ESPCEX 2009 - Questões

Sete livros didáticos, cada um de uma disciplina diferente, devem ser posicionados lado a lado em uma estante, de forma que os livros de Física, de Química e de Matemática estejam sempre juntos, em qualquer ordem. O número de maneiras diferentes em que esses livros podem ser posicionados é

Um agricultor, que dispõe de $60$ metros de tela, deseja cercar uma área retangular, aproveitando-se de dois trechos de muro, sendo um deles com $12$ metros de comprimento e o outro com comprimento suficiente, conforme a figura abaixo.

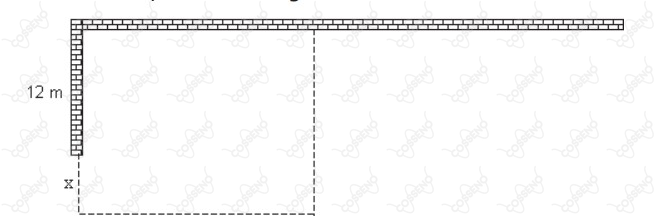
Sabendo que ele pretende usar exatamente os $60$ metros de tela, pode-se afirmar que a expressão que representa a área cercada $y$, em função da dimensão $x$ indicada na figura, e o valor da área máxima que se pode obter nessas condições são, respectivamente, iguais a

Um dos modelos matemáticos de crescimento populacional é conhecido como “Modelo Malthusiano” (Thomas Malthus, 1766-1834). Neste modelo, a evolução de uma população é dada pela função $$P(t) = P_0 · K^t$$ em que $P_0$ é a população inicial, $k$ indica a taxa de crescimento (considerada constante e não negativa neste modelo) e $t$ é o tempo decorrido.

Um biólogo que estudava uma cultura de bactérias observou que, oito horas após o início do experimento, a população era de $8000$ indivíduos e que, duas horas depois dessa observação, a população era de $16000$ indivíduos. Podemos afirmar que a população inicial era de

Dentre as várias formas de se medir temperatura, destacam-se a escala Celsius, adotada no Brasil, e a escala Fahrenheit, adotada em outros países. Para a conversão correta de valores de temperaturas entre essas escalas, deve-se lembrar que $0$ grau, na escala Celsius, corresponde a $32$ graus na escala Fahrenheit e que $100$ graus, na escala Celsius, correspondem a $212$ graus na escala Fahrenheit.

Para se obter um valor aproximado da temperatura, na escala Celsius, correspondente a uma temperatura conhecida na escala Fahrenheit, existe ainda uma regra prática definida por:

“divida o valor da temperatura em Fahrenheit por $2$ e subtraia $15$ do resultado.”

A partir dessas informações, pode-se concluir que o valor da temperatura, na escala Celsius, para o qual a regra prática fornece o valor correto na conversão é

Considere a função real $g(x)$ definida por:

$$ g(x) = \begin{cases} 5^x, \mathrm{se} \ x \leq 1 \\ \frac{-3x^2}{4} + \frac{3x}{2} + \frac{17}{4},\ \mathrm{se} \ 1 < x \leq 3 \\ \frac{x}{2} +\frac{1}{2}, \ \mathrm{se}\ x > 3 \end{cases}$$

O valor de g(g(g(1)) é: