ESPCEX 2007 - Questões

O valor de x que satisfaz a equação $x+\frac{2x}{3}+\frac{4x}{9}+\frac{8x}{27}+...=243$, em que o primeiro membro é uma P.G. infinita, é

Os termos da seqüência de números em progressão aritmética $\frac{\pi}{3},\frac{7\pi}{12},\frac{5\pi}{6}...$ correspondem às medidas em radianos de arcos, que podem ser representados na circunferência trigonométrica abaixo. Os pontos identificados por $0$ a $VII$ representam as medidas de arcos que dividem a circunferência trigonométrica em $8$ partes iguais, medidas no sentido anti-horário, a partir de $0$.

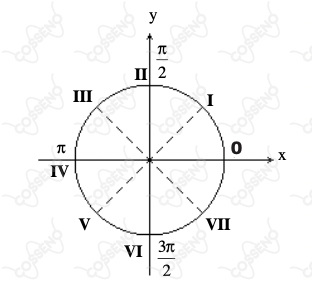
Nessas condições, o arco correspondente ao 13° termo da seqüência, igualmente medido no sentido anti-horário e a partir de 0, terá sua extremidade situada entre os pontos

A quantidade de números $inteiros\ ímpares$ que pertencem ao intervalo que satisfaz a inequação exponencial $\left(\frac{1}{2}\right)^{x^2-8x+5}>4$ é de

Num determinado setor de um hospital, trabalham 4 médicos e 8 enfermeiras. O número de equipes distintas, constituídas cada uma de 1 médico e 3 enfermeiras, que podem ser formadas nesse setor é de

Em uma bolsa existem peças em formatos de triângulos, quadrados e pentágonos, nas quantidades de $x$ triângulos, $y$ quadrados e $z$ pentágonos. Sabendo-se que a soma das quantidades de peças é igual a $10$; que, se somarmos as quantidades de vértices de todas as peças, obtemos $37$; e que a quantidade de triângulos é igual à soma das quantidades de quadrados e pentágonos, o valor de $2x + 3y + z$ é igual a: