EPCAR 2020 Matemática - Questões

Considere as expressões $P$ e $Q$, com os números $a$, $b$ e $c$ reais positivos e distintos entre si.

$$P = \dfrac{(a^6 + b^6 + c^6)^2 - (a^6 - b^6 -c^6)^2}{b^6 + c^6}$$

$$Q = \dfrac{(b^{-1} - a^{-1})^{-1} - (b^{-1} + a^{-1})^{-1}}{(a^{-1} + b^{-1})^{-1}-(a^{-1}-b^{-1})^{-1}}$$

A expressão $\sqrt{Q\sqrt{P}}$ é representada por

Dona Lourdes trabalha em uma livraria, precisa guardar $200$ livros em $x$ caixas e vai utilizar todas elas.

Se em $30$ das $x$ caixas ela guardar $4$ livros em cada caixa e, nas demais, guardar $5$ livros em cada caixa, então, sobrarão alguns livros para serem guardados.

Entretanto, se em $20$ das $x$ caixas ela guardar $4$ livros em cada caixa e $5$ livros em cada uma das demais, então, não haverá livros suficientes para ocupar todas as caixas.

Assim, a soma dos algarismos do número $x$ é igual a

À noite, um helicóptero da Força Aérea Brasileira sobrevoa uma região plana e avista um $VANT$ (Veículo Aéreo Não Tripulado) de forma circular e altura desprezível, com raio de $3 \text{ m}$, estacionado paralelamente ao solo a $30 \text{ m}$ de altura.

O $VANT$ está a uma distância $y$ metros de um holofote que foi instalado no helicóptero.

O feixe de luz do holofote que ultrapassa o $VANT$ incide sobre a região plana e produz uma sombra circular de centro $O$ e raio $R$.

O raio $R$ da circunferência da sombra forma um ângulo de $60^\circ$ com o feixe de luz, conforme se vê na figura seguinte.

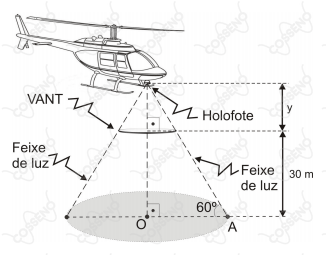
Nesse momento, uma pessoa que se encontra num ponto $A$ da circunferência da sombra corre para o ponto $O$, pé da perpendicular traçada do holofote à região plana.

A distância, em metros, que essa pessoa percorre de $A$ até $O$ é um número entre

Para homenagear os aniversariantes do mês de junho, um grupo de alunos das turmas FOX e GOLF do esquadrão SABRE decidem fazer um churrasco comemorativo e dividir a despesa total.

Na véspera do churrasco, $6$ desses alunos foram convocados pelo seu Comandante para uma atividade que os impediu de comparecerem ao evento comemorativo, sendo esses $6$ alunos excluídos do rateio da despesa total.

Com a ausência desses $6$ alunos, foi cobrado de cada um dos demais, certo valor a mais.

Ao fazerem o rateio, os alunos perceberam que a despesa total era igual ao valor cobrado a mais de cada um dos alunos que contribuíram, multiplicado por $180$.

Se o número de alunos que foram ao churrasco é $K$, então, a soma dos algarismos de $K$ é

Seja $S \subset \mathbb{R}$ o conjunto solução, na variável $x$, da equação irracional dada por $\sqrt[4]{\left(x^2 + x\right)^4 } + \sqrt[8]{\left(x^2 + 4\right)^4} = 420$

Sugestão: use $\left(x^2 + x\right) = y$

Analise as alternativas e marque a FALSA.