EN 2022 - Questões

Sejam $f$ e $g$ funções definidas nos reais, tais que $f(x) = 4x^3 - 24x^2 + 48x - 40$ e $f \circ g(x) = x$. Dessa forma $g(x)$ é igual a:

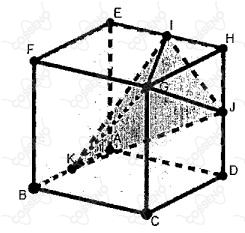
Seja o cubo $ABCDEFGH$ de aresta $2$ $\pu{cm}$ e $I, J$ e $K$ pontos médios das arestas $EH, DH$ e $AB$, respectivamente. O volume da pirâmide $GIJK$, em $\pu{cm3}$, é igual a:

Para que os valores reais de $x$, a sequência geométrica $\left( \frac{2x}{3x + 1}; \frac{2x}{(3x+1)^2}; \frac{2x}{(3x + 1)^3}; ... \right)$ possui o limite da soma de seus termos iguais a $\frac{2}{3}$ ?

Sejam as funções $f$ e $g$ tais que $f(x) = 5x^4 - 2x^3 + 2x$, $g'(x) = \frac{2}{x+3}$ e $g(1) = 0$. O valo de $(f \circ g)'(1)$ é igual a:

Seja $Z = \frac{\sqrt{3}}{2} + \frac{1}{2}i$ um número complexo, sendo $i$ a unidade imaginária.

Considere a soma $S = 1 + Z + Z^2 + Z^3 + ... + Z^{49} + Z^{50}$. Desse modo, assinale a opção que apresenta o intervalor $R$ ao qual a parte real de $S$ pertence. Dados: $\sqrt{2} = 1{,}4$, $\sqrt{3} = 1{,}7$ e $\sqrt{5} = 2{,}2$