EN 2021 Matemática - Questões

Um fabricante de bolas de tênis (bolas em formatos esféricos) deseja vender as bolas em embalagens cilíndricas (cilindros circulares retos) de raio $R$ e altura $H$, cada uma. Em cada embalagem há $n$ bolas de tênis de raio $R$, cada bola. O fabricante deseja que a área total das superfícies das bolas seja igual à área lateral da embalagem (cilindro). Dessa forma, é correto afirmar que:

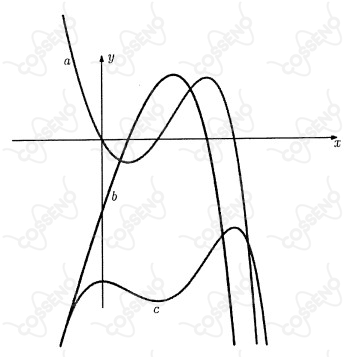
Seja $f$ uma função real e $f'$ e $f''$ as derivadas de ordem um e dois, respectivamente. A figura abaixo mostra parte dos gráficos de $f, f'$ e $f''$, indicados pelas letras $a$, $b$ e $c$. Dessa forma, assinale a opção que apresenta uma correspondência correta.

Seja a sequência abaixo definida por uma lei de recorrência de $3^a$ ordem. Cada termo dessa sequência (do quarto termo em diante) é uma combinação linear dos três termos imediatamente anteriores.

$$(2, -1, 1, 6, 3, -1, \cdots).$$

A soma do sétimo termo com o oitavo termo é igual a

Assinale a opção que apresenta a soma de todas as coordenadas dos pontos da reta $r: x - 1 = 2y = z$ que equidistam dos planos $\pi_1 : 2x - 3y - 4z - 3 = 0$ e $\pi_2: 4x - 3y - 2z = -3$.

Um dos mais brilhantes trabalhos do matemático grego Arquimedes ($287$ a.C. - $212$ a.C.) foi a Quadratura da Parábola. Através do Método da Exaustão, Arquimedes demonstrou que a área de um segmento parabólico (região compreendida entre a parábola e uma linha reta $r$), conforme figura abaixo.

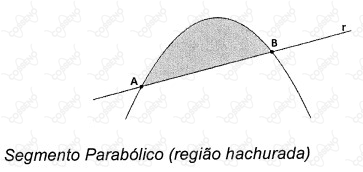
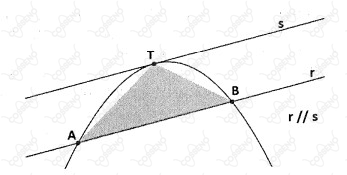
Essa área do segmento parabólico equivale a $\frac{4}{3}$ da área do triângulo $ABT$ seguinte, inscrito no segmento parabólico, sendo as retas $r$ e $s$ paralelas e $T$ o ponto de tangência.

Seja $p$ uma parábola com foco $F\left(-\frac{\sqrt 2}{2}; \frac{3\sqrt 2}{2}\right)$ e reta diretriz $d: x + y + \sqrt 2 = 0$. A parábola é seccionada pela reta $r: \sqrt{2}\cdot x + \sqrt{2} \cdot y - 8 = 0$, originando a região hachurada da figura abaixo.

Com base nas informações apresentadas, é correto afirmar que a área da região hachurada é igual a