Um dos mais brilhantes trabalhos do matemático grego Arquimedes ($287$ a.C. - $212$ a.C.) foi a Quadratura da Parábola. Através do Método da Exaustão, Arquimedes demonstrou que a área de um segmento parabólico (região compreendida entre a parábola e uma linha reta $r$), conforme figura abaixo.

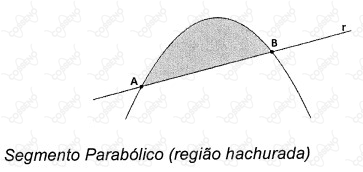
Essa área do segmento parabólico equivale a $\frac{4}{3}$ da área do triângulo $ABT$ seguinte, inscrito no segmento parabólico, sendo as retas $r$ e $s$ paralelas e $T$ o ponto de tangência.

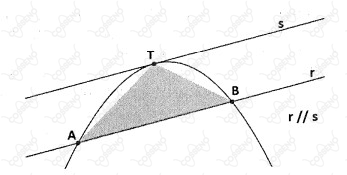
Seja $p$ uma parábola com foco $F\left(-\frac{\sqrt{2}}{2};\frac{3\sqrt{2}}{2}\right)$ e reta diretriz $d:x+y+\sqrt{2}=0$. A parábola é seccionada pela reta $r:\sqrt{2}\cdot x+\sqrt{2}\cdot y-8=0$, originando a região hachurada da figura abaixo.

Com base nas informações apresentadas, é correto afirmar que a área da região hachurada é igual a