EN 2018 Matemática - Questões

Dadas as matrizes: $$A=\begin{bmatrix}&1 &2 &-1\\&1 &0 &1\\&1 &-1 &1\end{bmatrix},\ x=\begin{bmatrix}2\ \ \ 13\ \ \ 65\end{bmatrix}\ \ e\ \ B=x^{\gamma}\cdot x$$ Qual é o valor do determinante de $2\cdot A^{-1}\cdot B^2?$

Determine o valor do limite $lim_{x\rightarrow -\infty}\frac{(x+\sqrt[3]{1-x^3})}{2}$ e assinale a opção correta

Sejam $h,\ p,\ f$ e $g$ funções reais tais que $h(x) = |x|+ |x-1|$, $p(x)=x^3$, $f(x)=x^2$ e $g(x)=ax^3)$, com $a>0$.0 valor de $\alpha$ torna a área da região limitada por $f$ e $g$, no intervalo $[0,\frac{1}{\alpha}]$ igual a $\frac{2}{3}$ é o valor da área da região limitada por $h,\ p$ e pelo eixo das ordenadas. Assinale a opção que representa um número inteiro.

O atual campeão carioca de futebol, Botafogo, possui escudo baseado em um pentagrama, conforme figuras abaixo.

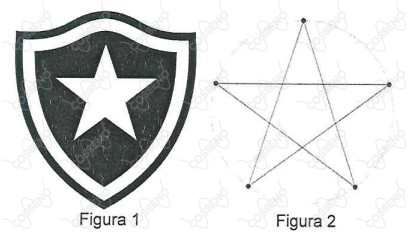
O pentagrama é um polígono estrelado de 5 vértices, que podem ser igualmente distribuídos em uma circunferência (formando cinco arcos congruentes). O pentagrama, através de seus segmentos, determina 6 regiões internas, 5 triângulos e 1 pentágono. O pentágono é vizinho de todos os triângulos e não existem triângulos vizinhos entre si. Sendo assim, utilizando até 6 cores distintas (preto, branco, cinza, verde, amarelo e azul), de quantas maneiras essas regiões do pentagrama, conforme Figura 2, podem ser coloridas, de forma que não haja duas regiões vizinhas com cores iguais?

Observe a figura abaixo.

O cubo $ABCDEFGH$, de aresta $\pu{3 cm}$, é rotacionado em torno de sua diagonal $AG$, gerando um sólido de revolução de volume $V$. Dessa forma, pode-se afirmar que o valor de $V$, em $cm^3$, é tal que: