CN 2021 - Questões

Filtro de Questões

Abrir Opções Avançadas

Filtrar por resolução:

01 CN 2021 - Matemática

Observe a figura a seguir:

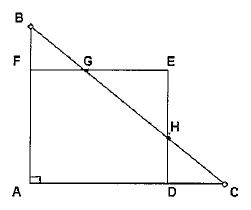
Na figura, $ABC$ é um triângulo retângulo de catetos $p$ e $q$ e hipotenusa $s$, $ADEF$ é um quadrado de lado unitário com vértice $E$ externo ao triângulo $ABC$. Utilizando $p$, $q$ e $s$ para representar a soma $\overline{FG} + \overline{DH}$ obtém-se:

02 CN 2021 - Matemática

Considerando os resultados das expressões $A$ e $B$ até a 4ª casa decimal sem fazer aproximações e sabendo-se que:

$A = \dfrac{(11\%\ \text{de } 25)+36\%\ \text{de}\ (75 \cdot 3\%\ \text{de}\ 50)}{(24\%\ \text{de}\ 35) - (8\%\ \text{de}\ 40) } = 8,a1b3$ e

$B = \dfrac{(75\%\ \text{de}\ 36\times 50\%\ \text{de}\ 3)+(25\%\ \text{de}\ 11) }{(35\%\ \text{de}\ 24) - (40\%\ \text{de}\ 8)} = c,3d7e$,

Assim, determine o resto da divisão de $N$ por $11$ sendo o número $N=(a+b)^{c+d+e}$.

03 CN 2021 - Matemática

Suponha que durante a pandemia uma distribuidora de medicamentos tivesse estoque de álcool gel com distribuições diárias iguais, suficiente para atender $18$ farmácias durante $64$ dias. Após $16$ dias, $6$ farmácias fecharam e, passados mais $17$ dias, a distribuidora aceitou um pedido do governo para que atendesse a mais $10$ farmácias. As farmácias fechadas não irão abrir mais. É correto afirmar que a partir do dia em que aceitou o pedido do governo a distribuidora terá estoque suficiente para atender a todas as farmácias durante:

04 CN 2021 - Matemática

Considere o conjunto $A = \{x \ | \ x = \dfrac{1}{n +1}, n \in \mathbb{N}\}$ um subconjunto da reta. É correto afirmar que:

existe um único elemento de $A$ cuja distância a qualquer outro elemento, também de $A$, é inferior a qualquer número real positivo.

zero é um elemento do conjunto $A$.

fixado qualquer valor real positivo $p$, sempre existirão dois elementos do conjunto $A$ cuja distância na reta real é menor do que $p$.

existe um elemento do conjunto $A$ que não é racional.

existem dois elementos do conjunto $A$, de tal modo que a diferença entre eles não é um número racional.

05 CN 2021 - Matemática

Observe a figura a seguir.

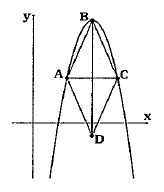
Na figura, a parábola é a representação gráfica no plano cartesiano da função $y= - x^2 + 14x - 33$. Sabe-se, sobre o losango $ABCD$ de diagonais $\overline{AC}$ e $\overline{BD}$, com $\overline{AC}$ paralelo ao eixo de $x$ e $BD$ paralelo ao eixo de $y$, que o produto das abscissas dos vértices $A$ e $C$ é igual a $40$ e que o vértice $B$ é o ponto de ordenada máxima da função. É correto afirmar que a área do losango em unidades de área é igual a:

Carregando...