AFA 2019 Física - Questões

Três partículas, $A$, $B$ e $C$, movimentam-se, com velocidades constantes, ao longo de uma mesma direção. No instante inicial, $t_0 = 0$, a distância entre $A$ e $B$ vale $x$, e entre $B$ e $C$ vale $\pu{y}$, conforme indica a figura a seguir.

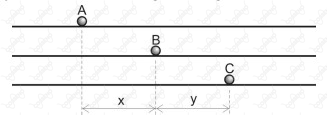
Em $t = \pu{2 s}$, a partícula $A$ cruza com a partícula $B$. Em $t = \pu{3 s}$, a partícula $A$ cruza com a partícula $C$. A partícula $C$ alcançará a partícula B no instante dado pela relação

Uma partícula, de massa $\pu{1 kg}$, descreve um movimento circular uniformemente variado, de raio $\pu{2,25 m}$, iniciando-o a partir do repouso no instante $t_0 = 0$.

Em $t = \pu{2 s}$, o módulo de sua velocidade vetorial $( \vec{v} )$ é de $\pu{6 m/s}$, conforme figura abaixo.

A intensidade da força resultante sobre a partícula, no instante $t = 1 s$, em $\pu{N}$, vale

Considere dois sistemas térmicos $A$ e $B$ constituídos de corpos perfeitamente esféricos, em condições normais de temperatura e pressão, conforme figura abaixo.

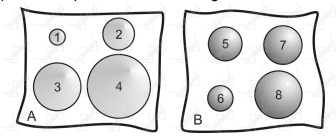
No sistema $A$, as esferas $1, 2, 3\ \text{e}\ 4$ são pequenas gotas esféricas de água pura com massa respectivamente iguais a $\pu{1 g}, \pu{2 g}, \pu{4 g}\ \text{e}\ \pu{8 g}$. O sistema $B$ é constituído das esferas maciças e homogêneas $5, 6, 7\ \text{e}\ 8$ de mesmo material, de calor específico constante igual a $\pu{0,2 cal/g ^{\circ} C}$ e massa específica igual a $\pu{2,5 g/cm^3}$ . Os volumes dessas esferas são conhecidos e valem, respectivamente, $4, 5, 7\ \text{e}\ \pu{16 cm^3}$ . Nessas condições, o número máximo de esferas do sistema A que podem ser permutadas simultaneamente com esferas do sistema $B$, de maneira que os sistemas $A$ e $B$ continuem com a mesma capacidade térmica inicial e com o mesmo número de esferas, é

Uma esfera, de dimensões desprezíveis, sob ação de um campo gravitacional constante, está inicialmente equilibrada na vertical por uma mola. A mola é ideal e se encontra com uma deformação $x$, conforme ilustrado na figura 1.

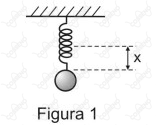
O sistema esfera-mola é posto, em seguida, a deslizar sobre uma superfície horizontal, com velocidade constante, conforme indicado na figura 2. Nessa situação, quando o ângulo de inclinação da mola é $\theta$ , em relação à horizontal, sua deformação é $y$.

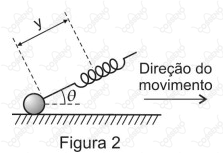
Nessas condições, o coeficiente de atrito cinético entre a esfera e a superfície horizontal vale

A montagem da figura a seguir ilustra a descida de uma partícula 1 ao longo de um trilho curvilíneo. Partindo do repouso em $A$, a partícula chega ao ponto $B$, que está a uma distância vertical $4H$ abaixo do ponto $A$, de onde, então, é lançada obliquamente, com um ângulo de $45{^\circ}$ com a horizontal.

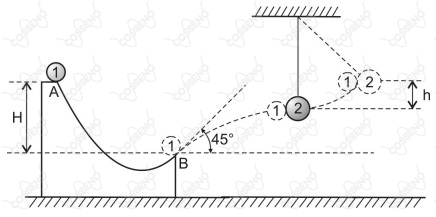
A partícula, agora, descreve uma trajetória parabólica e, ao atingir seu ponto de altura máxima, nessa trajetória, ela se acopla a uma partícula 2, sofrendo, portanto, uma colisão inelástica.

Essa segunda partícula possui o dobro de massa da primeira, está em repouso antes da colisão e está presa ao teto por um fio ideal, de comprimento maior que $H$, constituindo, assim, um pêndulo. Considerando que apenas na colisão atuaram forças dissipativas, e que o campo gravitacional local é constante. O sistema formado pelas partículas 1 e 2 atinge uma altura máxima $h$ igual a