AFA 2019 - Questões

Considere no plano cartesiano abaixo representadas as funções reais $f : \bigl ]m,-m \bigr] \rightarrow \pu{IR} \text{e g} : \bigl [m,-m\bigr[ - \bigl\{v\bigr\} \rightarrow \pu{IR}$

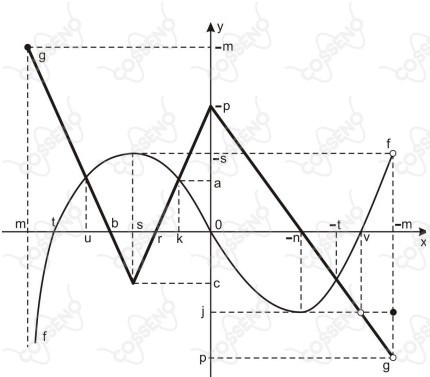
Nas afirmativas abaixo, escreva V para verdadeira e F para falsa.

$(\ \ )$ O conjunto imagem da função g é dado por $\text{Im}(g)=\bigl]p,-m\bigr]$

$(\ \ )$A função h definida por $h ( x ) = f ( x ) \cdot g ( x )$ assume valores não negativos somente se $x \in \bigl [t,b \bigr] \cup \bigl [r,0\bigr]

$(\ \ )$A função $j$ definida por $j ( x ) = g ( x ) − p$ é maior que zero para todo $x \in \bigl (\bigl [m , − m\bigr [ - \bigl\{v\bigr\}\bigr)$

A sequência correta é

Um objeto de decoração foi elaborado a partir de sólidos utilizados na rotina de estudos de um estudante de matemática.

Inicialmente, partiu-se de um cubo sólido de volume igual a $\pu{19683 cm^3}$

Do interior desse cubo, retirou-se, sem perda de material, um sólido formado por dois troncos de pirâmide idênticos e um prisma reto, como mostra o esquema da figura a seguir.

Sabe-se que:

• as bases maiores dos troncos estão contidas em faces opostas do cubo;

• as bases dos troncos são quadradas;

• a diagonal da base maior de cada tronco está contida na diagonal da face do cubo que a contém e mede a sua terça parte;

• a diagonal da base menor de cada tronco mede a terça parte da diagonal da base maior do tronco; e

• os troncos e o prisma têm alturas iguais.

Assim, o volume do objeto de decoração obtido da diferença entre o volume do cubo e o volume do sólido esquematizado na figura acima, em $\pu{cm^3}$ , é um número do intervalo

Sobre a inequação $\frac{3 x^2 + 2 x}{x}\ge x^3$, considerando o conjunto universo $\cup\subset \pu{IR}$, é INCORRETO afirmar que possui conjunto solução

O domínio mais amplo da função real f definida por $f ( x ) =\sqrt{\log_a\left({x²-3}\right)}$ , em que $\text{a} \in \biggl ] 0,1\biggr[ $, é

Considere, no plano cartesiano, a figura abaixo, em que os segmentos horizontais são paralelos ao eixo $\overleftrightarrow{O_x}$ e os segmentos verticais são paralelos ao eixo $\overleftrightarrow{O_y}$

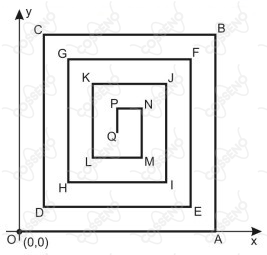
Sabe-se que:

• os comprimentos de segmentos consecutivos da poligonal, que começa na origem $O ( 0 , 0 )$ e termina em $Q$ , formam uma progressão aritmética decrescente de razão $\pu{r}$ e primeiro termo a 1 , em que $\bigl(-\frac{1}{15}<r<0\bigr)$;

• dois comprimentos consecutivos da poligonal são sempre perpendiculares;

• $\overline{OA} = a_1$ , $\overline{AB} = a_2$ , $\overline{BC} = a_3$ , e, assim sucessivamente, até $\overline{PQ} = a_{16}$

Suponha que uma formiga parta da origem $O ( 0 , 0 )$ , e percorra a trajetória descrita pela poligonal até chegar ao ponto $Q$

Com base nas informações acima, analise as proposições abaixo.

$\pu{I}$. Se $a_1 = 1\ \text{e}\ r=- \frac{1}{16}$, então a distância d percorrida pela formiga pela formiga até chegar ao ponto $Q$ é tal que $\pu{d} =\frac{17}{2}a_1$

$\pu{II}$. Quando a formiga estiver na posição do ponto $L ( x , y )$, então $x = − 6 r$

$\pu{III}$. Se $a_ 1 = 1$ , então de $A$ até $C$ , a formiga percorrerá a distância $d = 2 + 3 r$

Quanto a veracidade das proposições, tem-se