AFA 2017 Física - Questões
Abrir Opções Avançadas
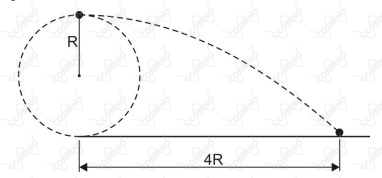
Uma partícula de massa $m$, presa na extremidade de uma corda ideal, descreve um movimento circular acelerado, de raio $R$, contido em um plano vertical, conforme figura a seguir.Quando essa partícula atinge determinado valor de velocidade, a corda também atinge um valor máximo de tensão e se rompe. Nesse momento, a partícula é lançada horizontalmente, de uma altura $2R$, indo atingir uma distância horizontal igual a $4R$. Considerando a aceleração da gravidade no local igual a $g$, a tensão máxima experimentada pela corda foi de
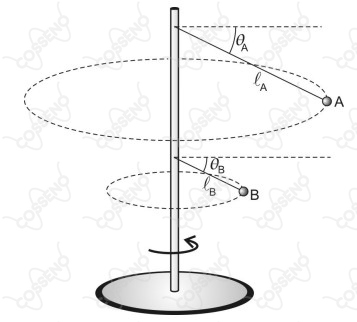
Dois pequenos corpos $A$ e $B$ são ligados a uma haste rígida através de fios ideais de comprimentos $\ell_{a}$ e $\ell_{b}$ , respectivamente, conforme figura a seguir.
$A$ e $B$ giram em sincronia com a haste, com velocidades escalares constantes $\text{v}_{A}$ e $\text{v}_{B}$ , e fazem com a direção horizontal ângulos $\theta_{A}$ e $\theta_{B}$ , respectivamente.
Considerando $\ell_{a}$=${4}\ell_{b}$ , a razão $\frac {\text v_A}{\text v_B}$ , em função de $\theta_{A}$ e
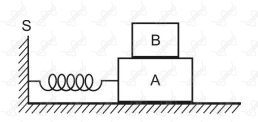
Na situação da figura a seguir, os blocos $A$ e $B$ têm massas $\text m_A = \pu {3,0 kg}$ e $\text m_B= \pu {1,0 kg}$ . O atrito entre o bloco $A$ e o plano horizontal de apoio é desprezível, e o coeficiente de atrito estático entre $B$ e $A$ vale $\mu_e=0,4$. O bloco $A$ está preso numa mola ideal, inicialmente não deformada, de constante elástica $K = \pu{160N/m}$ que, por sua vez, está presa ao suporte $S$.
O conjunto formado pelos dois blocos pode ser movimentado produzindo uma deformação na mola e, quando solto, a mola produzirá uma certa aceleração nesse conjunto. Desconsiderando a resistência do ar, para que $B$ não escorregue sobre $A$, a deformação máxima que a mola pode experimentar, em $\pu {cm}$, vale
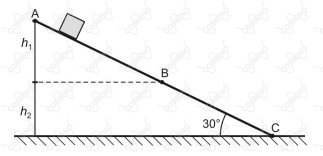
Um bloco escorrega, livre de resistência do ar, sobre um plano inclinado de $\pu 30^\circ$, conforme a figura (sem escala) a seguir.
No trecho $AB$ não existe atrito e no trecho $BC$ o coeficiente de atrito vale $\mu=\frac{\sqrt3}{2}$.
O bloco é abandonado, do repouso em relação ao plano inclinado, no ponto $A$ e chega ao ponto $C$ com velocidade nula. A altura do ponto $A$, em relação ao ponto $B$, é $h_1$ , e a altura do ponto $B$, em relação ao ponto $C$, é $h_2$ . A razão $\frac {h_1}{h_2}$ vale
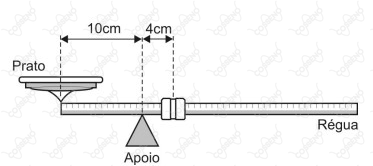
Em feiras livres ainda é comum encontrar balanças mecânicas, cujo funcionamento é baseado no equilíbrio de corpos extensos. Na figura a seguir tem-se a representação de uma dessas balanças, constituída basicamente de uma régua metálica homogênea de massa desprezível, um ponto de apoio, um prato fixo em uma extremidade da régua e um cursor que pode se movimentar desde o ponto de apoio até a outra extremidade da régua. A distância do centro do prato ao ponto de apoio é de $\pu{10cm}$. O cursor tem massa igual a $\pu{0,5kg}$. Quando o prato está vazio, a régua fica em equilíbrio na horizontal com o cursor a $\pu{4cm}$ cm do apoio.
Colocando $\pu{1kg}$ sobre o prato, a régua ficará em equilíbrio na horizontal se o cursor estiver a uma distância do apoio, em $\pu{cm}$, igual a
Carregando...