AFA 2016 - Questões

O lado EF de uma espira condutora quadrada indeformável, de massa m, é preso a uma mola ideal e não condutora, de constante elástica K. Na posição de equilíbrio, o plano da espira fica paralelo ao campo magnético $\vec{B}$ gerado por um ímã em forma de U, conforme ilustra a figura abaixo.

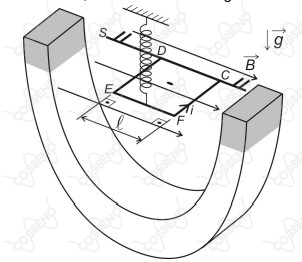
O lado CD é pivotado e pode girar livremente em torno do suporte S, que é posicionado paralelamente às linhas de indução do campo magnético. Considere que a espira é percorrida por uma corrente elétrica i, cuja intensidade varia senoidalmente, em função do tempo t, conforme indicado no gráfico abaixo.

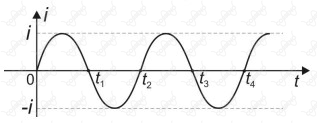
Nessas condições, pode-se afirmar que a

O diagrama abaixo ilustra os níveis de energia ocupados por elétrons de um elemento químico $A$. Dentro das possibilidades apresentadas nas alternativas abaixo, a energia que poderia restar a um elétron com energia de $\pu{12,0 eV}$, após colidir com um átomo de $A$, seria de, em $\pu{eV}$

Dois mecanismos que giram com velocidades angulares $\omega_{1}$ e $\omega_{2}$ constantes são usados para lançar horizontalmente duas partículas de massas $m_{1}=\pu{1kg}$ e $m_{2}=\pu{2kg}$ de uma altura $h=\pu{30m}$, como mostra a figura $1$ abaixo.

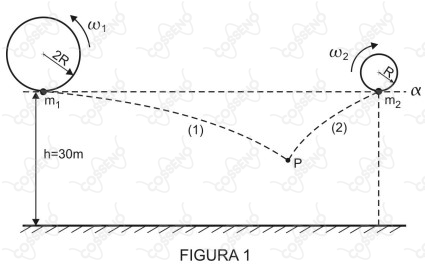
Num dado momento em que as partículas passam, simultaneamente, tangenciando o plano horizontal $\alpha$ , elas são desacopladas dos mecanismos de giro e, lançadas horizontalmente, seguem as trajetórias $1$ e $2$ (figura $1$) até se encontrarem no ponto P.

Os gráficos das energias cinéticas, em joule, das partículas $1$ e $2$ durante os movimentos de queda, até a colisão, são apresentados na figura $2$ em função de $( h − y )$ , em m, onde $y$ é a altura vertical das partículas num tempo qualquer, medida a partir do solo perfeitamente horizontal.

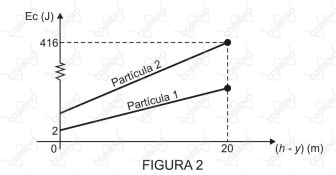
Desprezando qualquer forma de atrito, a razão $\dfrac{\omega_2}{\omega_1}$ é

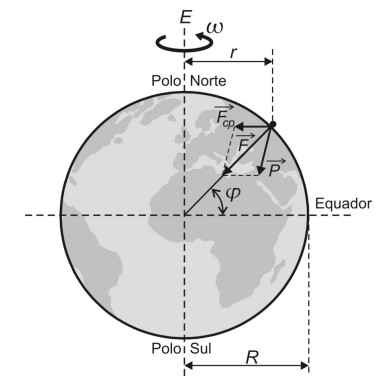
Considere a Terra um Planeta esférico, homogêneo, de raio $R$, massa $M$ concentrada no seu centro de massa e que gira em torno do seu eixo $E$ com velocidade angular constante $\omega$ , isolada do resto do universo. Um corpo de prova colocado sobre a superfície da Terra, em um ponto de latitude $\phi$ , descreverá uma trajetória circular de raio r e centro sobre o eixo E da Terra, conforme a figura abaixo. Nessas condições, o corpo de prova ficará sujeito a uma força de atração gravitacional $\vec{F}$ , que admite duas componentes, uma centrípeta,$\vec{F}_{cp}$ , e outra que traduz o peso aparente do corpo, $\vec{P}$ .Quando $\varphi = 0°$ , então o corpo de prova está sobre a linha do equador e experimenta um valor aparente da aceleração da gravidade igual a $g_{e}$ . Por outro lado, quando $\varphi = 90°$ , o corpo de prova se encontra em um dos Polos, experimentando um valor aparente da aceleração da gravidade igual a $g_{p}$ . Sendo G a constante de gravitação universal, a razão $\dfrac {g_e}{g_p}$ vale

Deseja-se aquecer $\pu{1,0 L}$ de água que se encontra inicialmente à temperatura de $\pu{10 °C}$ até atingir $\pu{100 °C}$ sob pressão normal, em $\pu{10 minutos}$, usando a queima de carvão. Sabendo-se que o calor de combustão do carvão é $\pu{6000 cal/g}$ e que $80\%$ do calor liberado na sua queima é perdido para o ambiente, a massa mínima de carvão consumida no processo, em gramas, e a potência média emitida pelo braseiro, em watts, são