AFA 2014 Matemática - Questões
Abrir Opções Avançadas
A equação $x^3 - 4x^2 +5x+3=0$ possui as raizes m, p e q.
O valor da expressão $\frac{m}{pq}+\frac{p}{mq}+\frac{q}{mp}$ é
Distribuiu-se, aleatoriamente, 7 bolas iguais em 3 caixas diferentes. Sabendo-se que nenhuma delas ficou vazia, a probabilidade de uma caixa conter, exatamente, 4 bolas é
Considere os gráficos abaixo das funções reais $f:A\rightarrow ℝ$ e $g:B\rightarrow ℝ$.
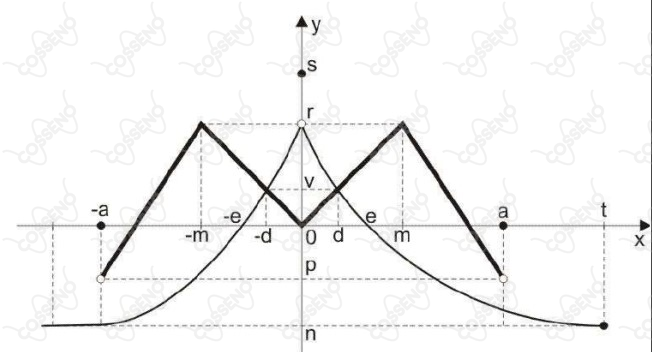
Sabe-se que $A=[a, a];\ \ \ \ B= ]-\infty, t];\ \ \ \ g(-a)< f(-a);\ \ \ \ g(o)>f(0);\ \ g(a)<f(a)\ \ e\ \ g(x)=n$ para todo $x\leq -a$.
Analise as afirmativas abaixo e marque a FALSA.
Sejam f e g funções reais dadas por $f(x)=\left|\frac{\sin{2x}}{\cos{x}}\right|$ e $g(x)=2$, cada uma definida no seu domínio mais amplo possível. Analise as afirmações abaixo.
I) O conjunto solução da equação $f(x)=g(x)$ contém infinitos elementos.
II) No intervalo $\left[\frac{3\pi}{4},\frac{5\pi}{4}\right]$
III) O período da função $f$ é $p=\pi$
Sobre as afirmações é correto afirmar que
Uma escultura de chapa de aço com espessura desprezível foi feita utilizando-se inicialmente uma chapa quadrada de 1 metro de lado apoiada por um de seus vértices sobre um tubo cilíndrico. A partir desse quadrado, a escultura foi surgindo nas seguintes etapas:
$1^a)$ Em cada um dos 3 vértices livres do quadrado foi construído um quadrado de lado $\frac{1}{2}$ metro.
$2^a)$ Em cada um dos vértices livres dos quadrados construídos anteriormente, construiu-se um quadrado de lado $\frac{1}{4}$ de metro
E assim, sucessivamente, em cada vértice livre dos quadrados construídos anteriormente, construiu-se um quadrado cuja medida do lado é a metade da medida do lado do quadrado anterior. A figura seguinte esquematiza a escultura nas etapas iniciais de sua confecção.
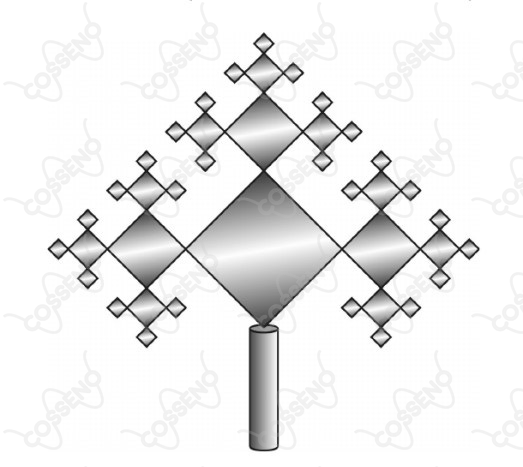
Considerando que a escultura ficou pronta completadas sete etapas, é correto afirmar que a soma das áreas dos quadrados da $7^a$ etapa é igual a
Carregando...