AFA 2003 - Questões

Considere a função real definida por $y=\frac{\cos2x}{1+\sin2x}$ e as seguintes afirmações:

1. A função é decrescente em todo seu domínio

2. O gráfico da função apresenta assíntotas nos arcos $\frac{\pi}{2}+k\pi$, $k$

3. A função negativa em $\left[0,\frac{\pi}{4}\right[$

4. A função admite inversa em $\left[0,\frac{\pi}{2}\right]$

   São verdadeiras somente as afirmações contidas nos itens

$ABC$ é um triângulo retângulo em $A$ e $\overline{CX}$ é bissetriz do ângulo $BĈA$, onde $X$ é ponto do lado $\overline{AB}$ . A medida $\overline{CX}$ é $4 \pu{cm}$ e a de $\overline{BC}$ , $24 \pu{cm}$. Sendo assim, a medida do lado $\overline{AC}$ , em centímetros, é igual a

O valor do determinante de uma matriz de ordem $n$ é $21$. Se dividirmos a segunda linha desta matriz por $7$ e multiplicarmos a matriz por $3$, o valor do novo determinante será

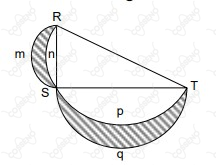
Na figura, $RST$ é um triângulo retângulo em $S$. Os arcos $RnSpT$, $RmS$ e $SqT$ são semicircunferências cujos diâmetros são, respectivamente, $RT$, $SR$ e $ST$. A soma das áreas das figuras hachuradas está para a área do triângulo $RST$ na razão

Seja $P$ uma pirâmide cujo vértice é o centro de uma das faces de um cubo de aresta $\textbf{a}$ e cuja base é a face oposta. Então, a área lateral dessa pirâmide é igual a