AFA 2002 - Questões

Uma das raízes da equação (I) $4x^3 -12x^2 -x + m = 0 $ ($m \in \mathbb{R}$) é a solução da equação (II) $\tan{\frac{\pi x}{12}} = 1$ no intervalo $[0, \pi]$. Então, pode-se afirmar que o produto das raízes da equação (I) vale

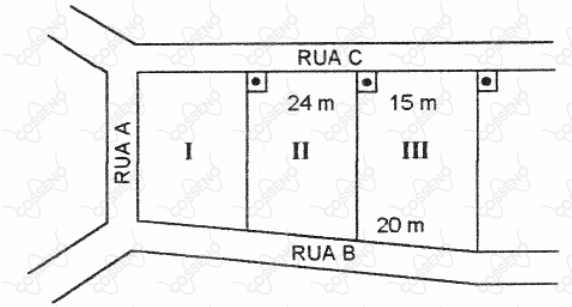
No desenho abaixo, estão representados os terrenos I, II, III.

Quantos metros de comprimento deverá ter o muro que o proprietário do terreno II construirá para fechar o lado que faz frente coma rua $B$?

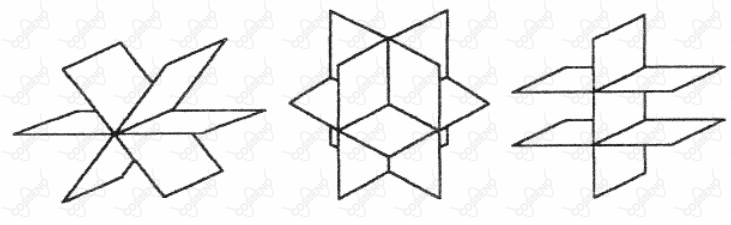
O conjunto de soluções de uma única equação linear $a_1x + a_2y + a_3z = b$ é representado por um plano no sistema de coordenadas retangulares $xyz$ (quando $a_1$, $a_2$, $a_3$ não são todos iguais a zero). Analise as figuras a seguir.

(I) $\space$ Três planos se cortando numa reta

(II) $\space$ Três planos se cortando num ponto

(III) $\space$ Três planos sem interseção

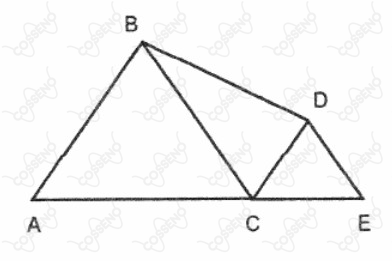
Na figura abaixo, os triângulos $ABC$ e $CDE$ são equiláteros. Se a razão entre as áreas desses triângulos é $\frac{9}{4}$ e o perímetro do menor é $12$, então, a área do quadrilátero $ABDE$ é

A área total do sólido gerado pela rotação do polígono $ABCDE$ em torno do eixo y, que contém o lado $AE$, é, em $\pu m^2$, igual a