AFA 1999 - Questões

Um alvo para tiro é formado por três círculos concêntricos de raios $10$, $20$ e $\pu{30 cm}$. Se os pontos atribuídos a cada área forem inversamente proporcionais às probabilidades de acerto, o conjunto dos menores valores inteiros possíveis para estes pontos é:

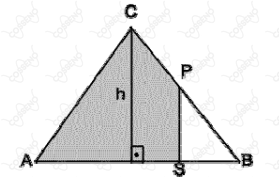
Na figura abaixo, $\overline{AC} = \overline{BC}$, $h = \overline{AB} = 10$ e $\overline{SP}$ é perpendicular a $\overline{AB}$. O ponto $S$ percorre $\overline{AB}$ e $\overline{AS} = x$. Nessas condições, a área da figura sombreada pode ser expressa por:

Seja $AB$ um diâmetro de um circuito de centro $O$, $C$ o centro do círculo de diâmetro $OA$ e $CO$ diâmetro do círculo que tangencia interiormente o círculo de centro $C$. Então, a razão da área do maior círculo para a do menor vale:

Os valores de $k$ para que a reta que passa pelos pontos $(5, k)$ e $(1, 0)$ seja paralela à reta definitiva pelos pontos $(-2, 1)$ e $(k, 3)$:

Sabendo-se que a elipse $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$, $a > 0$ e $b > 0$, passa pelos pontos $(2, 3)$ e $(0, 3\sqrt{2})$, então $a + b$ vale: