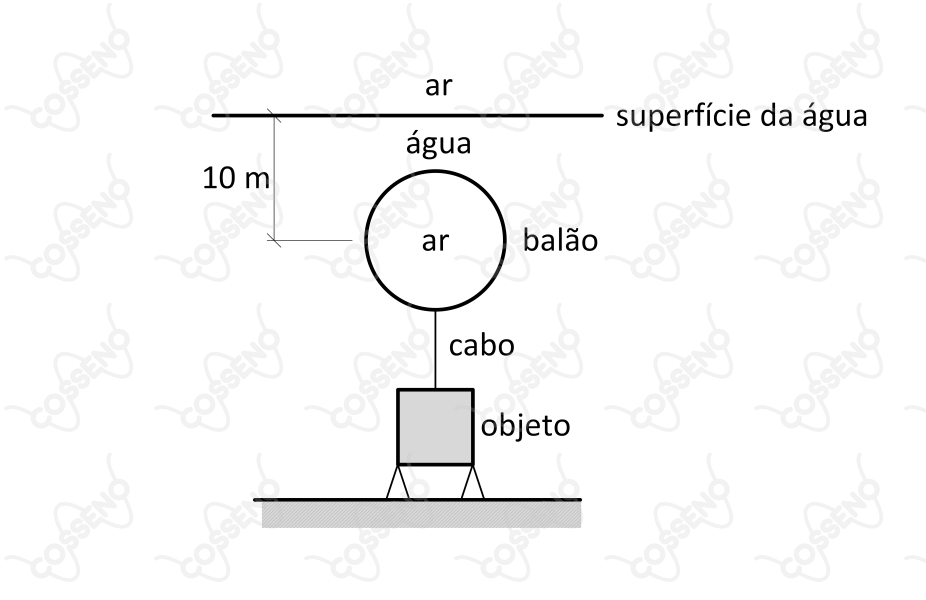
Um objeto de formato cúbico, com aresta de comprimento e de massa específica , encontra-se apoiado no fundo do mar, devendo ser içado por meio de um balão de borracha de massa , que apresenta volume interno de ar ajustável. A figura ilustra a situação descrita, com o centro do balão posicionado a de profundidade. O volume do balão, em , relaciona-se com a diferença de pressão , em atm, entre a pressão interna e a externa do balão pela seguinte equação:para .
A pressão interna mínima do balão, em atm, a partir da qual será iniciado o movimento do objeto é:
Dados:
• massa do balão: $m_b = 50\ kg$;
• massa do cabo: $m_c = 100\ kg$;
• comprimento da aresta do objeto cúbico: $L = 1\ m$;
• aceleração da gravidade: $g = 10\ m/s^2$;
• massa específica do objeto: $\mu_{obj} = 2850\ kg/m^3$;
• massa específica da água: $\mu_{agua} = 1000\ kg/m^3$; e
• $1\ atm = 10^5\ Pa$.
Observações:
• o ar acima da superfície da água encontra-se a $1\ atm$ de pressão;
• desconsidere o volume do cabo e a massa do ar internamente ao balão; e
• para efeito do cálculo da pressão hidrostática sobre o balão
considere que todo o volume $V$ esteja posicionado na mesma profundidade de seu centro.
considere que todo o volume $V$ esteja posicionado na mesma profundidade de seu centro.