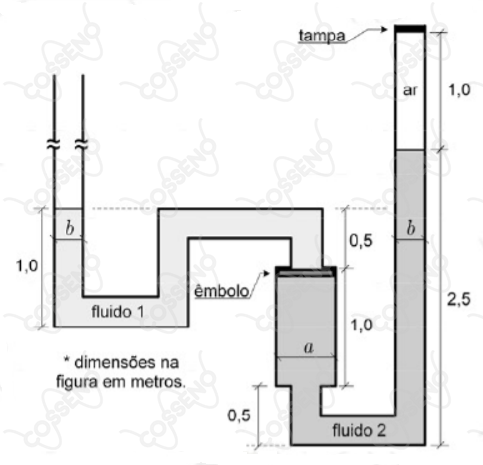
Um tubo com seção reta interna quadrada de lado contém dois fluidos incompressíveis em equilíbrio, separados por um êmbolo, conforme a situação ilustrada na figura. A cavidade em que o êmbolo se desloca, sem atrito, apresenta seção reta interna quadrada de lado . O êmbolo é formado por um material indeformável, com massa, espessura e volume desprezíveis, e encontra-se, inicialmente, na posição superior dentro da cavidade. Em certo instante, a segunda extremidade do tubo é perfeitamente vedada com uma tampa, mantendo o ar confinado com a mesma pressão atmosférica externa.
Considerando que não ocorrerão mudanças de temperatura nos fluidos e no ar confinado, para que o êmbolo entre em equilíbrio abaixo da posição inicial, quantos litros do fluido deverão ser inseridos na extremidade aberta do tubo?