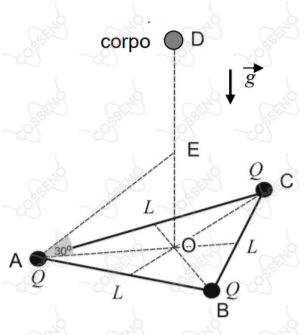
A figura apresenta três esferas de cargas positivas fixas nos vértices de um triângulo equilátero de centro e localizado no plano horizontal. Um corpo de massa , posicionado no ponto em , tem a ele grudadas milhares de micropartículas de cargas positivas e massas desprezíveis. O corpo sofre uma queda vertical até o ponto . No intervalo , diversas micropartículas vão se soltando gradativamente do corpo, de modo que sua velocidade permanece constante. O restante das micropartículas desprende-se totalmente em , exatamente no ponto , no qual o ângulo entre os segmentos e é de . O corpo continua em movimento até atingir o plano no ponto em .
Determine:
a) a velocidade do corpo no intervalo ;
b) a altura inicial do corpo (comprimento ) em ;
c) a carga do corpo imediatamente antes do instante , quando o restante das micropartículas se desprendeu;
d) a carga inicial do corpo em .
- considere a massa do corpo constante
- despreze as dimensões do corpo
- ao se desprenderem$,$ as cargas das micropartículas não influenciam no movimento do corpo.
Dados:
- massa do corpo: $m = 2{,}7 \ kg$
- cargas fixas nos vértices do triângulo: $Q = 10^{-4} \ C$
- aceleração da gravidade: $g = 10 \ m/s^{2}$
- constante dielétrica do meio: $k = 9 \times 10^{9} \ {{Nm^{2}}/{C^{2}}}$
- comprimentos dos lados do triângulo: $L = 24 \ m$.