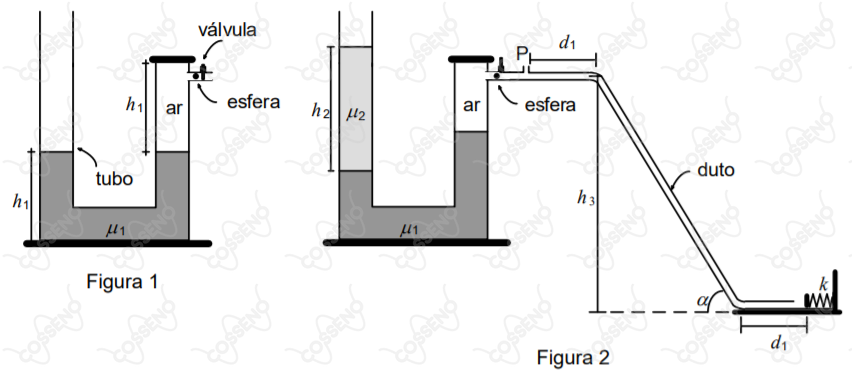
Um tubo rígido aberto nas extremidades, com seção reta de área constante, é preenchido com um fluido de massa específica até alcançar a altura . O tubo é lacrado em uma das extremidades, conforme ilustra a Figura , imediatamente acima de uma válvula, que se encontra fechada, de modo que a coluna de ar também tenha altura e esteja com a mesma pressão atmosférica externa. A haste da válvula mantém presa uma esfera que se ajusta bem ao duto de saída, com seção reta circular. Um segundo fluido, de massa específica , é lentamente colocado na extremidade aberta até formar uma coluna de altura , conforme mostra a Figura .
Em determinado instante, a válvula é subitamente aberta, liberando a esfera, que é impulsionada pelo ar comprimido por um breve intervalo de tempo , até atingir o ponto . A esfera percorre o trajeto dentro do duto até alcançar uma mola, de constante elástica , que se deforma .
Com relação à situação apresentada, determine:
a) a pressão da coluna confinada de ar, em , supondo a temperatura constante, após a inserção do segundo fluido e antes da abertura da válvula.
b) a força de atrito média a partir do ponto , em , que age na esfera em sua trajetória até alcançar a mola.
- considere constante a pressão que impulsiona a esfera durante seu movimento até o ponto $P$
- após o ponto $P$
o interior do duto encontra-se à pressão atmosférica
- não há força de atrito durante a compressão da mola
- não há atrito no movimento da esfera entre a válvula e o ponto $P$.
Dados:
- aceleração da gravidade: $g = 10 \ m/s^{2}$
- alturas: $h_1 = 1 \ m$; $h_2 = 1{,}75 \ m$; e $h_3 = 4 \ m$
- ângulo $\alpha = 30^{\circ}$
- área da seção reta do duto: $S_{d} = 1 \ cm^{2}$
- constante elástica da mola: $k = 2.000 \ N/m$
- deformação máxima da mola: $= 2{,}5 \ cm$
- distância $d_1 = 1 \ m$
- intervalo de tempo que a esfera é impulsionada: $\Delta t = 0{,}1 \ s$
- massa da esfera: $m = 50 \ g$
- massas específicas: $\mu_{1} = 2.500 \ kg/m^{3}$; e $\mu_{2} = 2.000 \ kg/m^{3}$
- pressão atmosférica local: $P_{a} = 105 \ N/m^{2}$.