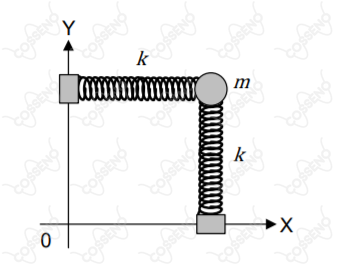
Uma partícula, inicialmente em repouso sobre o plano horizontal , está presa a duas molas idênticas, cada uma solidária em sua outra extremidade a um cursor que pode movimentar-se sobre seu respectivo eixo, como mostrado na figura. As molas são rígidas o suficiente para se deflexionarem apenas nas direções ortogonais de seus respectivos eixos aos quais estão presas. No instante , a partícula é puxada para o ponto de coordenadas e é lançada com velocidade inicial .
Determine:
a) as equações das componentes de posição, velocidade e aceleração da partícula nos eixos e , em função do tempo;
b) a área no interior da trajetória percorrida pela partícula durante o movimento.
Dados:
- massa da partícula: $m$
- constante elástica das molas: $k$
- $\omega = \sqrt{\frac{k}{m}}$
- comprimento das molas não flexionadas: $L$
Observações:
- o plano $XY$ é totalmente liso
- não há influência da gravidade no movimento da partícula
- os cursores deslizam sem atrito pelos eixos
- as coordenadas $X$ e $Y$ da partícula são sempre positivas.
- massa da partícula: $m$
- constante elástica das molas: $k$
- $\omega = \sqrt{\frac{k}{m}}$
- comprimento das molas não flexionadas: $L$
Observações:
- o plano $XY$ é totalmente liso
- não há influência da gravidade no movimento da partícula
- os cursores deslizam sem atrito pelos eixos
- as coordenadas $X$ e $Y$ da partícula são sempre positivas.