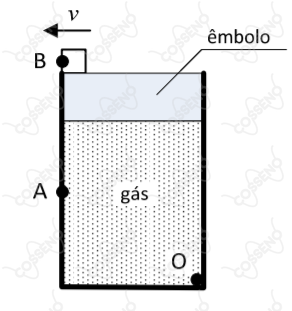
A figura acima mostra um recipiente com paredes transparentes de espessuras desprezíveis. Esse recipiente contém um gás ideal hipotético e é fechado por um êmbolo opaco. Inicialmente, um corpo encontra-se apoiado sobre o êmbolo, em sua extremidade, mantendo todo o sistema em equilíbrio. Uma microcâmera, posicionada no ponto (interior do recipiente) e direcionada para o ponto , consegue filmar o ponto no corpo.

O corpo é, então, lançado com velocidade horizontal e sem atrito. Após o lançamento do corpo, o gás se expande até que o êmbolo atinja o equilíbrio novamente em um intervalo de tempo desprezível. A temperatura permanece constante durante todo o fenômeno. Determine em quanto tempo, após o lançamento, o corpo voltará a ser filmado pela microcâmera.

Observação: • o êmbolo tem altura suficiente para permanecer vedando o recipiente durante toda a expansão do gás;
• considere que o gás obedeça à lei de Gladstone-Dale$,$ que diz que a relação entre seu índice de refração $n$ e sua densidade $\rho$ é constante e dada pela expressão: $\frac{n-1}{\rho}=\ cte$.

Dados: • Altura inicial do ponto $B$: $90\ cm$; • Altura do ponto $A$: $30\ cm$ ; • Base do recipiente: Quadrado de lado $40\ cm$ ; • Massa do corpo = Massa do êmbolo ; • Velocidade $v$: $1,5\ m/s$ ; • Índice de refração do vácuo: $1,0$ ; e • Aceleração da gravidade: $10\ m/s^2$