A circunferência tem equação . Seja uma circunferência de raio que se desloca tangenciando internamente a circunferência , sem escorregamento entre os pontos de contato, ou seja, rola internamente sobre .
Define-se o ponto sobre de forma que no início do movimento de o ponto coincide com o ponto de tangência , conforme figura . Após certo deslocamento, o ângulo de entre o eixo e a reta que une o centro das circunferências é , conforme figura .
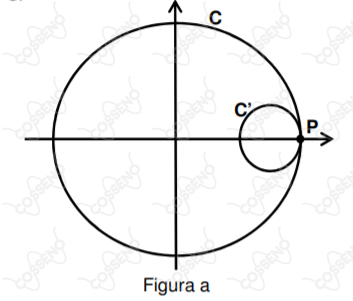
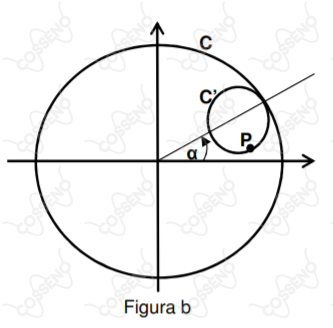
- Determine as coordenadas do ponto marcado sobre em função do ângulo .
- Determine a equação em coordenadas cartesianas do lugar geométrico do ponto quando a varia no intervalo .