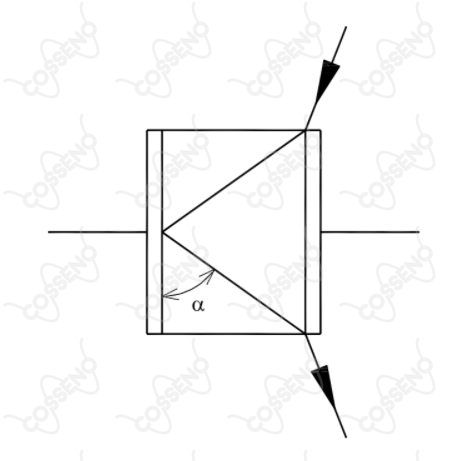
De acordo com a figura acima, um raio luminoso que estava se propagando no ar penetra no dielétrico de um capacitor, é refletido no centro de uma das placas, segundo um ângulo , e deixa o dielétrico. A área das placas é e o tempo que o raio luminoso passa no interior do dielétrico é . Supondo que se trata de um capacitor ideal de placas paralelas e que o dielétrico é um bloco de vidro que preenche totalmente o espaço entre as placas, determine a capacitância do capacitor em picofarads.
Dados:
•$A = 1,0\ cm^2$
•$t = 2,0 \times 10^{-12}\ s$
•$\alpha = 30^\circ$
•permissividade elétrica do vácuo: $\varepsilon_o \approx 9,0 \times 10^{-12}\ F/m$
•velocidade da luz no vácuo: $c \approx 3,0 \times 10^8\ m/s$
• índice de refração do vidro: $n = 1,5$
•constante dielétrica do vidro: $k = 5,0$
•$A = 1,0\ cm^2$
•$t = 2,0 \times 10^{-12}\ s$
•$\alpha = 30^\circ$
•permissividade elétrica do vácuo: $\varepsilon_o \approx 9,0 \times 10^{-12}\ F/m$
•velocidade da luz no vácuo: $c \approx 3,0 \times 10^8\ m/s$
• índice de refração do vidro: $n = 1,5$
•constante dielétrica do vidro: $k = 5,0$