Um objeto pontual luminoso que oscila verticalmente em movimento harmônico simples, cuja equação da posição é $y=A\cos (\omega t)$, é disposto paralelamente a um espelho esférico gausiano côncavo $(E)$ de raio de curvatura igual a $8A$, e a uma distância $3A$ de esspelho (Figura $1$).

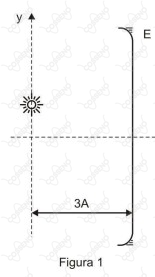
Um observador visualiza a imagem desse objeto conjugada pelo espelho e mede a amplitude $A_1$ e a frequência de oscilação do movimento dessa imagem.

Trocando-se apenas o espelho por uma lente esférica convergente delgada $(L)$ de distância focal $A$ e índice de refração $n=2$, (figura $2$), o mesmo observador visualiza uma imagem projetada do objeto oscilante e mede a amplitude $A_2$ e a frequência do movimento da imagem.

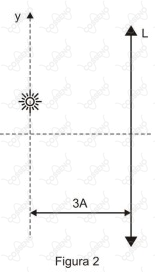
Considere que o eixo óptico dos dispositivos usados passe pelo ponto de equilíbrio estável do corpo que oscila e que as observações foram realizadas em um meio perfeitamente transparente e homogêneo de índice de refração igual a $1$.

Nessas condições, a razão entre as amplitudes $A_2$ e $A_1$, $\frac{A_2}{A_1}, de oscilação das imagens conjugadas pela lente e pelo espelho é