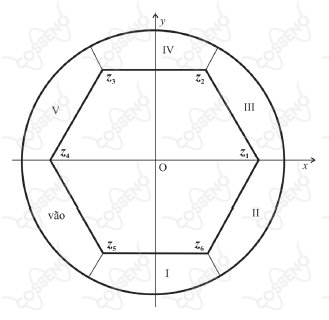
O Museu de Arte Contemporânea de Niterói possui aspectos geométricos interessantes. Um dos pisos contém um salão principal praticamente hexagonal; ao redor desse salão, há cinco galerias e um vão de entrada, que completam um círculo. Nos vértices do hexágono, existem pilastras de sustentação e, em cada uma das diagonais do hexágono, foram construídas vigas de reforço, abaixo do piso. A figura acima apresenta, em um sistema de coordenadas cartesianas ortogonais xOy, uma planta aproximada desse piso, com escala em metros. Cada ponto (x, y) do plano está associado a um número complexo z = x + iy, em que i é a unidade imaginária (i² = -1). As raízes complexas z₁, ..., z₆ da equação z⁶ = 14⁶ identificam a localização das pilastras de sustentação e também os vértices do hexágono que constitui o salão principal; as galerias (identificadas pelos números de I a V, na figura) e o vão de entrada, divididos radialmente, completam a circunferência, definida pela equação |z| = 17. A tabela a seguir apresenta as coordenadas de z₁, z₂ e z₃. As coordenadas de z₄, z₅ e z₆ podem ser obtidas por simetria. 

A partir dessas informações, julgue o item.

Um visitante percorrerá mais de 25 m se caminhar, em linha reta, do ponto z₄ até o ponto z₂.