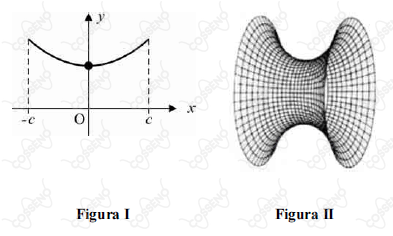
Um cabo flexível e homogêneo suspenso entre dois pontos, como as linhas telefônicas entre dois postes, forma uma curva denominada catenária, devido à ação exclusiva da força peso.
A figura I ilustra essa curva, em um sistema de coordenadas cartesianas ortogonais xOy, em que o ponto mais baixo da curva está sobre o eixo Oy. Nesse sistema, a catenária é o gráfico da função $y=f(x)=\frac{a}{2}\left[e^{bx}+e^{-bx}\right]$, em que a e b são constantes reais positivas e
e é a base do logaritmo natural.

A figura II mostra o sólido denominado catenoide, que pode ser obtido girando-se em torno do eixo Ox a região do plano xOy compreendida entre as retas x = -c e x = c, acima do eixo Ox e abaixo da catenária, representada na figura I. Esse sólido também pode ser obtido mergulhando-se, em uma solução de água e sabão, uma argola de arame e retirando-a em seguida.

A partir das informações acima, julgue o item.

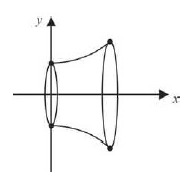
Considere que a figura abaixo ilustre um catenoide obtido pela rotação da catenária definida por y = f (x) = $\frac{1}{2}$$\left[e^x+e^{-x}\right]$ em torno do eixo Ox, para 0 ≤ x ≤ ln2. Se V₁ e V₂ são, respectivamente, os volumes dos cilindros inscrito e circunscrito a esse catenoide, no intervalo em questão, e se 3,14 e 0,69 são valores aproximados para B e ln 2, respectivamente, então o valor numérico de V₂ - V₁ é inferior a 1,3.