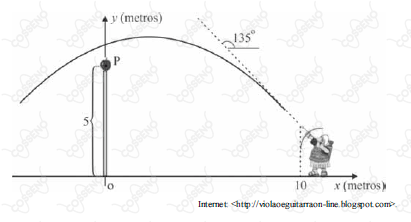
Em um sistema de coordenadas cartesianas ortogonais xOy, na situação da figura acima, a expressão $f(x)=\frac{23}{4}+\frac{x}{4}-\frac{x^2}{16}$ fornece a altura y = f(x), em metros, da ponta da flecha em função da abscissa x, em metros. Considere que, em cada instante t $ 0, em segundos, as coordenadas (x, f (x)) da trajetória descrita pela ponta de flecha podem ser dadas, em função de t, por (x(t), f (x(t))), com x(t) = 10 – 20t. Desse modo, o movimento da ponta da flecha se decompõe na horizontal como x(t) = 10 – 20t e, na vertical, como y(t) = f (x(t)).

Com base nessas informações, e considerando que uma maçã esteja localizada no ponto P de coordenadas (0, 5), julgue:
Considere que, em vez da flecha, o soldado estivesse utilizando uma arma de fogo com o cano apontado na mesma direção e sentido da flecha e que a trajetória do projétil fosse linear. Nessa situação, a distância, em metros, do ponto P à trajetória descrita pelo projétil seria igual a