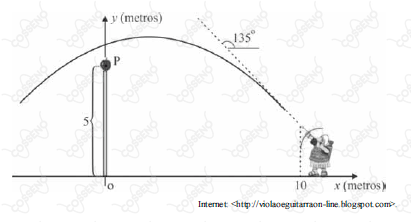
Em um sistema de coordenadas cartesianas ortogonais xOy, na situação da figura acima, a expressão f(x)=423+4x−16x2 fornece a altura y = f(x), em metros, da ponta da flecha em função da abscissa x, em metros. Considere que, em cada instante t 0,emsegundos,ascoordenadas(x,f(x))datrajetoˊriadescritapelapontadeflechapodemserdadas,emfunc\ca~odet,por(x(t),f(x(t))),comx(t)=10–20t.Dessemodo,omovimentodapontadaflechasedecompo~enahorizontalcomox(t)=10–20te,navertical,comoy(t)=f(x(t)).</p></div><div><p>Combasenessasinformac\co~es,econsiderandoqueumamac\ca~estejalocalizadanopontoPdecoordenadas(0,5),julgue:<br/>Suponhaqueosoldadotenhautilizadoumaarmadefogodemodoqueatrajetoˊriadoprojeˊtilsejalineareque,estandoapontadocanodaarmaaˋdista^nciade10metrosdosuportequesustentaamac\ca~eaumaalturade1a2metrosdosolo,oprojeˊtiltenhaatingidoamac\ca~.Nessasituac\ca~o,conclui−sequeoa^nguloentreatrajetoˊriadoprojeˊtileaflechaexibidanafigura,noinstantet=0,eˊinferiora \frac{\pi}{12}$ radianos.
