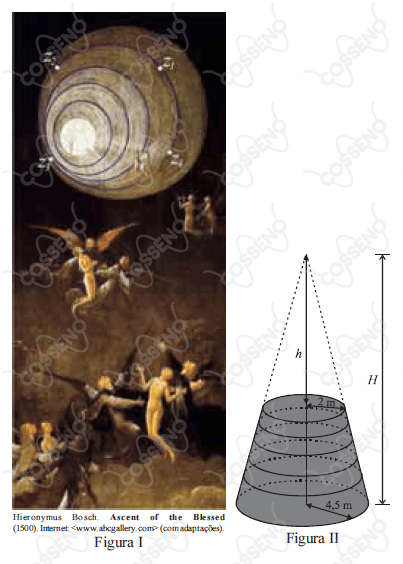
Considere que o túnel de luz na figura I seja formado pela sobreposição de cinco anéis de um mesmo cone circular reto — secções obtidas por planos perpendiculares ao eixo do cone —, tendo cada anel altura igual a 2 m, e sendo o maior e o menor raio interno medidos dentro do túnel iguais a 2 m e 4,5 m, respectivamente, conforme ilustrado na figura II. Considere, ainda, que, na figura I, z₁, z₂, z₃ e z₄ sejam números complexos que satisfazem à equação z₄ = 256. Com base nessas informações, julgue:

Identificando-se o número complexo z = x + iy com o ponto P = (x, y) em um sistema de coordenadas cartesianas xOy, a equação da circunferência que contém os pontos z₁, z₂, z₃ e z₄ será dada por x² + y² = 4.