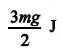
As campanhas bélicas do período helenístico contaram com inúmeras inovações tecnológicas, cujos fundamentos físicos e matemáticos foram desenvolvidos por cientistas como Arquimedes e Euclides. Uma dessas inovações foi a catapulta, que se baseia no princípio da alavanca e cujo modelo está ilustrado na figura acima. Nesse modelo, o comprimento do braço da catapulta, considerado totalmente rígido, é L = 3 m, e a movimentação desse braço realiza-se por meio de uma mola, de constante elástica k, que se comprime e se estende de acordo com o arco de circunferência de raio L, conforme mostrado na figura. Nessa figura, na posição em que o braço se encontra, a mola não está pressionada. Para que um projétil seja lançado com energia adequada, é necessário comprimir-se a mola de tal forma que seja igual a 30º o ângulo $\theta \le {\theta }_{max}$ — em que $\theta$ é o menor ângulo formado entre o eixo Ox e o braço da catapulta. Quando $\theta$ é igual a 30º, ele é denominado ângulo de compressão máxima.

Com base nessas informações, julgue o item a seguir.

Para um projétil de massa m considerado como partícula e posicionado no ponto P no momento de seu lançamento, o módulo da variação da energia potencial gravitacional entre a posição em que 2 = 30º e a posição em que não há compressão da mola — θ = θ_max — é igual a 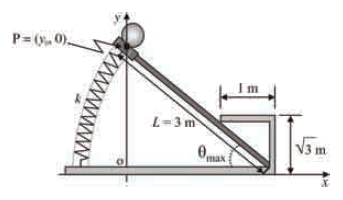 em que g representa a aceleração da gravidade