USP 2020 Física - Questões
Abrir Opções Avançadas
Um mol de um gás ideal monoatômico é resfriado adiabaticamente de uma temperatura inicial $T_1$ até uma temperatura final $\dfrac{T_1}{3}$.
Com base nessas informações, responda:
a) O gás sofreu expansão ou compressão ao final do processo? Justifique sua resposta.
b) Encontre o valor do trabalho realizado pelo gás nesse processo em termos da constante universal dos gases ideais $R$ e de $T_1$.
c) Encontre a razão entre as pressões final e inicial do gás após o processo.
Note e adote:
Em um processo adiabático, não há troca de calor com o ambiente.
Energia interna por mol de um gás ideal monoatômico: $U = \dfrac{3}{2}RT$.
Para o processo adiabático em questão, vale a relação $pV^\left( { \frac{5}{3}} \right)$ = constante.
A tomografia por emissão de pósitrons (PET) é uma técnica de imagem por contraste na qual se utilizam marcadores com radionuclídeos emissores de pósitrons. O radionuclídeo mais utilizado em PET é o isótopo 18 do flúor, que decai para um núcleo de oxigênio‐18, emitindo um pósitron. O número de isótopos de flúor‐18 decai de forma exponencial, com um tempo de meia-vida de aproximadamente $110\ minutos$.
A imagem obtida pela técnica de PET é decorrente da detecção de dois fótons emitidos em sentidos opostos devido à aniquilação, por um elétron, do pósitron resultante do decaimento. A detecção é feita por um conjunto de detectores montados num arranjo radial. Ao colidir com um dos detectores, o fóton gera cargas no material do detector, as quais, por sua vez, resultam em um sinal elétrico registrado no computador do equipamento de tomografia. A intensidade do sinal é proporcional ao número de núcleos de flúor‐18 existentes no início do processo.
a) Após a realização de uma imagem PET, o médico percebeu um problema no funcionamento do equipamento e o reparo durou $3h40\ min$. Calcule a razão entre a intensidade do sinal da imagem obtida após o reparo do equipamento e a da primeira imagem.
b) Calcule a energia de cada fóton gerado pelo processo de aniquilação elétron‐pósitron considerando que o pósitron e o elétron estejam praticamente em repouso. Esta é a energia mínima possível para esse fóton.
c) A carga elétrica gerada dentro do material do detector pela absorção do fóton é proporcional à energia desse fóton. Sabendo‐se que é necessária a energia de $3\ eV$ para gerar o equivalente à carga de um elétron no material, estime a carga total gerada quando um fóton de energia $600\ keV$ incide no detector.
Note e adote:
O elétron e o pósitron, sua antipartícula, possuem massas iguais e cargas de sinais opostos.
Relação de Einstein para a energia de repouso de uma partícula: $E = mc^2$.
Carga do elétron = $1,6\times10^{‐19}\ \text{C}$
Massa do elétron: $m = 9\times10^{‐31}\ \text{kg}$
Velocidade da luz: $c = 3\times10^8\ \text{m/s}$
$1\ \text{eV} = 1,6\times10^{‐19}\ \text{J}$
“Tempo de meia‐vida”: tempo necessário para que o número de núcleos radioativos caia para metade do valor inicial.
Em julho de 1969, os astronautas Neil Armstrong e Buzz Aldrin fizeram o primeiro pouso tripulado na superfície da Lua, enquanto seu colega Michael Collins permaneceu a bordo do módulo de comando Columbia em órbita lunar. Considerando que o Columbia estivesse em uma órbita perfeitamente circular a uma altitude de $260\ \text{km}$ acima da superfície da Lua, o tempo decorrido (em horas terrestres ‐ h) entre duas passagens do Columbia exatamente acima do mesmo ponto da superfície lunar seria de:
adote:
Constante gravitacional: $G = 9 \cdot 10^{-13}\ \text{km}^3/(\text{kg h}^2)$;
Raio da Lua = $1.740\ \text{km}$;
Massa da Lua $= 8 \cdot 10^{22}\ \text{kg}$
$\pi \cong 3$
Em $20$ de maio de $2019$, as unidades de base do Sistema Internacional de Unidades ($SI$) passaram a ser definidas a partir de valores exatos de algumas constantes físicas. Entre elas, está a constante de Planck $h$, que relaciona a energia $E$ de um fóton (quantum de radiação eletromagnética) com a sua frequência $f$ na forma $E = h\cdot f$.
A unidade da constante de Planck em termos das unidades de base do $SI$ (quilograma, metro e segundo) é:
A transmissão de dados de telefonia celular por meio de ondas eletromagnéticas está sujeita a perdas que aumentam com a distância $d$ entre a antena transmissora e a antena receptora. Uma aproximação frequentemente usada para expressar a perda $L$, em decibéis ($dB$), do sinal em função de $d$, no espaço livre de obstáculos, é dada pela expressão
$$L = 20 \cdot \log_{10}\ \left(\dfrac{4 \cdot \pi \cdot d}{\lambda}\right)$$
em que $\lambda$ é o comprimento de onda do sinal. O gráfico a seguir mostra $L$ (em $dB$) versus $d$ (em metros) para um determinado comprimento de onda $\lambda$.
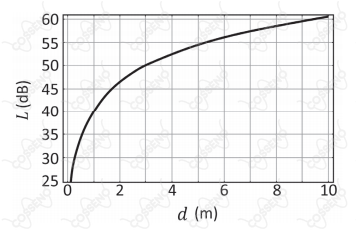
Com base no gráfico, a frequência do sinal é aproximadamente
Note e adote:
Velocidade da luz no vácuo:
$c = 3\cdot 10^{8}\ \text{m/s}$;
$\pi \cong 3$;
$1\ \text{GHz} = 10^{9}\ \text{Hz}$.
Carregando...