USP 2019 - Questões

Se a função $f: \mathbb{R}-\{2\}\ \to\ \mathbb{R}$ é definida por $f(x)= \dfrac{2x+1}{x-2}$ e a função $g: \mathbb{R}- \{2\}\ \to\ \mathbb{R}$ é definida por $g(x)=f(f(x))$, então $g(x)$ é igual a

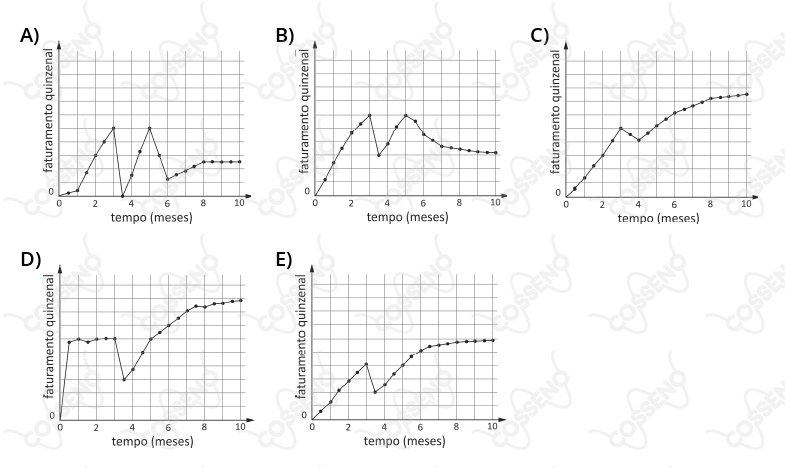
Um dono de restaurante assim descreveu a evolução do faturamento quinzenal de seu negócio, ao longo dos dez primeiros meses após a inauguração: “Até o final dos três primeiros meses, tivemos uma velocidade de crescimento mais ou menos constante, quando então sofremos uma queda abrupta, com o faturamento caindo à metade do que tinha sido atingido. Em seguida, voltamos a crescer, igualando, um mês e meio depois dessa queda, o faturamento obtido ao final do terceiro mês. Agora, ao final do décimo mês, estamos estabilizando o faturamento em um patamar $50\%$ acima do faturamento obtido ao final do terceiro mês”.

Considerando que, na ordenada, o faturamento quinzenal está representado em unidades desconhecidas, porém uniformemente espaçadas, qual dos gráficos é compatível com a descrição do comerciante?

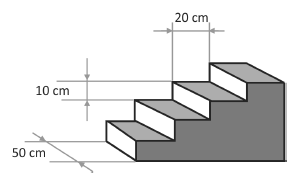
A figura mostra uma escada maciça de quatro degraus, todos eles com formato de um paralelepípedo reto‐retângulo. A base de cada degrau é um retângulo de dimensões $20\ \text{cm}$ por $50\ \text{cm}$, e a diferença de altura entre o piso e o primeiro degrau e entre os degraus consecutivos é de $10\ \text{cm}$. Se essa escada for prolongada para ter $20$ degraus, mantendo o mesmo padrão, seu volume será igual a

Se $\log_2\ {y}=- \dfrac{1}{2}+ \dfrac{2}{3} \cdot \log_2\ { x}$, para $x>0$, então

Uma seta aponta para a posição zero no instante inicial. A cada rodada, ela poderá ficar no mesmo lugar ou mover‐se uma unidade para a direita ou mover‐se uma unidade para a esquerda, cada uma dessas três possibilidades com igual probabilidade.

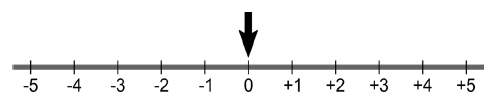
Qual é a probabilidade de que, após $5$ rodadas, a seta volte à posição inicial?