UNESP 2017 Matemática - Questões

Leia a matéria publicada em junho de 2016.

Energia eólica deverá alcançar 10 GW nos próximos dias

O dia mundial do vento, 15 de junho, terá um marco simbólico este ano. Antes do final do mês, a fonte de energia que começou a se tornar realidade no país há seis anos alcançará 10 GW, sendo que o potencial brasileiro é de 500 GW. A perspectiva é a de que, em metade deste tempo, o Brasil duplique os 10 GW.

(Disponível em:www.portalabeeolica.org.br. Adaptado.)

Considerando que a perspectiva de crescimento continue dobrando a cada três anos, calcule o ano em que o Brasil atingirá $64$% da utilização do seu potencial eólico. Em seguida, calcule o ano aproximado em que o Brasil atingirá $100$% da utilização do seu potencial eólico, empregando um modelo exponencial de base $2$ e adotando $\log\ 2\ =\ 0,3$ no cálculo final.

O hexágono marcado na malha quadriculada sobre a fotografia representa o contorno do campus da Unesp de Rio Claro, que é aproximadamente plano.

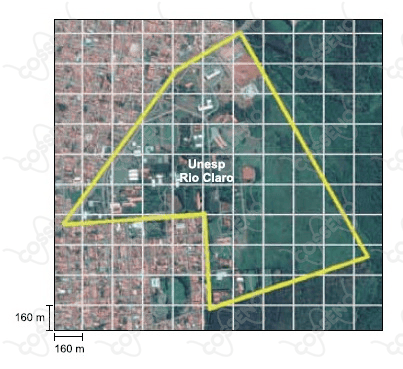
A área aproximada desse câmpus, em $km^2$, é um número pertencente ao intervalo

Uma companhia de engenharia de trânsito divulga o índice de lentidão das ruas por ela monitoradas de duas formas distintas, porém equivalentes. Em uma delas, divulga-se a quantidade de quilômetros congestionados e, na outra, a porcentagem de quilômetros congestionados em relação ao total de quilômetros monitorados.

O índice de lentidão divulgado por essa companhia no dia 10 de março foi de 25% e, no mesmo dia e horário de abril, foi de $200\ km$. Sabe-se que o total de quilômetros monitorados pela companhia aumentou em 10% de março para abril, e que os dois dados divulgados, coincidentemente, representavam uma mesma quantidade de quilômetros congestionados na cidade. Nessas condições, o índice de congestionamento divulgado no dia 10 de abril foi de, aproximadamente,

A figura indica o empilhamento de três cadeiras idênticas e perfeitamente encaixadas umas nas outras, sendo $h$ a altura da pilha em relação ao chão.

(www.habto.com. Adaptado.)

A altura, em relação ao chão, de uma pilha de $n$ cadeiras perfeitamente encaixadas umas nas outras, será igual a $1,4\ m$ se $n$ for igual a

No universo dos números reais, a equação $\dfrac{\left(x^2-13x+40\right)\left(x^2-13x\ +\ 42\right)}{\sqrt{x^2\ -\ 12x\ +\ 35\ }}=0$ é satisfeita por apenas