UNESP 2014 Matemática - Questões

Determine o período da função $f(\theta )$ dada pela lei de formação $f\left(\theta \right)=\dfrac{(-1)}{5}\cdot \hspace{2pt}\mathrm{sen}\ \left(\dfrac{2\theta}{3} -\dfrac{\pi }{3}\right)-1.$

Determine os zeros do polinômio $p(x)\ =\ x^3\ +\ 8$ e identifique a que conjunto numérico eles pertencem.

A figura mostra um relógio de parede, com $40\ cm$ de diâmetro externo, marcando 1 hora e 54 minutos.

Usando a aproximação $\pi =3$, a medida, em cm, do arco externo do relógio determinado pelo ângulo central agudo formado pelos ponteiros das horas e dos minutos, no horário mostrado, vale aproximadamente

Observe o espectro de radiação eletromagnética com a porção visível pelo ser humano em destaque. A cor da luz visível ao ser humano é determinada pela frequência $\text{v}$, em Hertz ($\text{Hz}$).

No espectro, a unidade de comprimento de onda $\lambda$ é o metro ($\text{m}$) e, no destaque, é o nanômetro ($\text{nm}$).

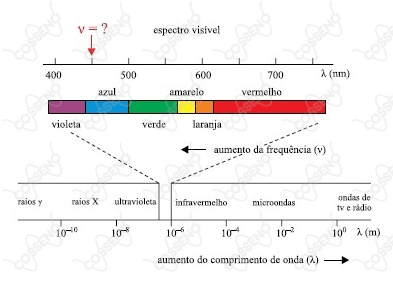
Sabendo que a frequência $\text{v}$ é inversamente proporcional ao comprimento de onda $\lambda$, sendo a constante de proporcionalidade igual à velocidade da luz no vácuo de, aproximadamente, $3,0\ \times \ {10}^8\ \text{m/s}$, e que $1$ nanômetro equivale a $1,0\ \times \ {10}^{-9}\ \text{m}$, pode-se deduzir que a frequência da cor, no ponto do destaque indicado pela flecha, em $\text{Hz}$, vale aproximadamente

Prato da culinária japonesa, o temaki e um tipo de sushi na forma de cone, enrolado externamente com nori, uma espécie de folha feita a partir de algas marinhas, e recheado com arroz, peixe cru, ovas de peixe, vegetais e uma pasta de maionese e cebolinha.

Um temaki típico pode ser representado matematicamente por um cone circular reto em que o diâmetro da base mede $8\ cm$ e a altura $10\ cm$. Sabendo-se que, em um temaki típico de salmão, o peixe corresponde a 90% da massa do seu recheio, que a densidade do salmão e de $0,35\ g/cm^{3}$, e tomando $\pi =3$, a quantidade aproximada de salmão, em gramas, nesse temaki, é de