UNESP 2010 Matemática - Questões
Abrir Opções Avançadas
Paulo quer comprar um sorvete com $4$ bolas em uma sorveteria que possui três sabores de sorvete: chocolate, morango e uva. De quantos modos diferentes ele pode fazer a compra?
No Brasil, desde junho de 2008, se for constatada uma concentração de álcool no sangue acima de $0,6g/l$, o motorista é detido e processado criminalmente.
(www.planalto.gov.br/ccivil$\_$03/Ato2007-2010/2008/Decreto/D6488.htm. Adaptado)
Determine o número máximo de latas de cerveja que um motorista pode ingerir, antes de dirigir, para não ser processado criminalmente caso seja submetido ao teste.
Dados:
O volume médio de sangue no corpo de um homem adulto é 7,0 litros;
Uma lata de cerveja de $350\ ml$ contém $16\ ml$ de álcool;
14% do volume de álcool ingerido por um homem adulto vão para a corrente sanguínea;
A densidade do álcool contido em cervejas é de$\ 0,8\ g/ml$.
Observação: Os resultados de todas as operações devem ser aproximados por duas casas decimais.
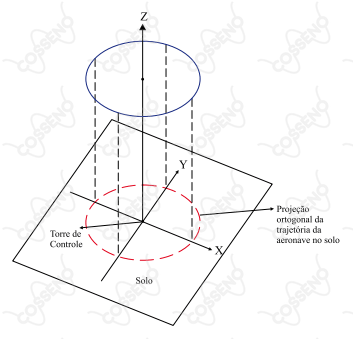
Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1 500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de $V_c\ (km/h)$, decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar.
Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.
Observe o gráfico da função $f(x)$ e analise as afirmações a seu respeito.
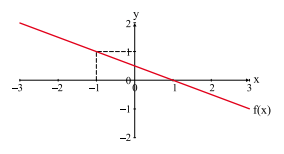
I) Se $x_1,x_2\in Dom(f)$ e $x_2>x_1$, então $f\left(x_2\right)>f\left(x_1\right)$.
II) Se $x>1$, então $f\left(x\right)<0$.
III) O ponto $(2,-2)$ pertence ao gráfico de $f(x)$.
IV) A lei de formação de $f(x)$ representada no gráfico é dada por $f\left(x\right)=-\dfrac{1}{2}(x-1)$.
A alternativa que corresponde a todas as afirmações verdadeiras é
O papelão utilizado na fabricação de caixas reforçadas é composto de três folhas de papel, coladas uma nas outras, sendo que as duas folhas das faces são “lisas” e a folha que se intercala entre elas é “sanfonada”, conforme mostrado na figura.
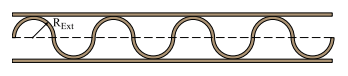
O fabricante desse papelão compra o papel em bobinas, de comprimento variável. Supondo que a folha “sanfonada” descreva uma curva composta por uma sequência de semicircunferências, com concavidades alternadas e de raio externo ($R_{Ext}$) de $1,5\ mm$, determine qual deve ser a quantidade de papel da bobina que gerará a folha “sanfonada”, com precisão de centímetros, para que, no processo de fabricação do papelão, esta se esgote no mesmo instante das outras duas bobinas de $102\ m$ de comprimento de papel, que produzirão as faces “lisas”.
Dado: $\pi \ \approx \ 3,14.$
Carregando...