UFRGS 2020 Matemática - Questões

O valor de $\sqrt{\ \left(1 - \dfrac{1}{2}\right)\cdot \left(1-\dfrac{1}{3}\right)\cdot \left(1-\dfrac{1}{4}\right)\cdots \left(1-\dfrac{1}{100}\right)}$ é

Considere as seguintes afirmações sobre números racionais.

I - Se $0 < \dfrac{a}{b} < \dfrac{c}{d}$ então $\left(\dfrac{a}{b}\right)^2 < \left(\dfrac{c}{d}\right)^2$.

II - Se $\dfrac{a}{b} < 0 < \dfrac{c}{d}$, então $\dfrac{c}{d}+ \dfrac{a}{b} > 0$.

III - Toda fração da forma $\dfrac{a}{b}$ é irredutível.

Quais estão corretas?

Se a equação $x^2 + 2\cdot x - 8 = 0$ tem as raízes $a$ e $b$, então o valor de $\left( \dfrac{1}{a} + \dfrac{1}{b}\right)^2$ é

Na figura abaixo, tem-se um retângulo $ABCD$, de lados $\overline{AB} = 3$ e $\overline{AD} = 5$, e um triângulo equilátero $BEC$, construído sobre o lado $\overline{BC}$.

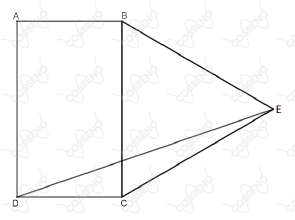
A medida de $\overline{DE}$ é

Considere dois círculos de centros $A$ e $C$, raio $1$ e tangentes entre si. O segmento $\overline{AC}$ é diagonal do quadrado $ABCD$. Os círculos de centros $B$ e $D$ são tangentes aos círculos de centros $A$ e $C$, como mostra a figura abaixo.

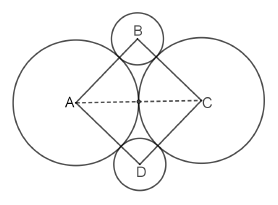
O raio dos círculos de centros $B$ e $D$ é