UERJ 2017 - Questões

Observe a matriz:

$$\left[\begin{array}{cc} {3+t} & {-4} \\ {3} & {t-4} \end{array}\right]$$

Para que o determinante dessa matriz seja nulo, o maior valor real de $t$ deve ser igual a:

Uma pirâmide com exatamente seis arestas congruentes é denominada tetraedro regular. Admita que a aresta do tetraedro regular ilustrado a seguir, de vértices $ABCD$, mede $6\ cm$ e que o ponto médio da aresta $\overline{BC}$ é $M$.

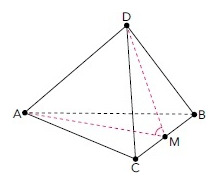
O cosseno do ângulo $A\hat{M}D$ equivale a:

Dois cubos cujas arestas medem $2\ cm$ são colados de modo a formar o paralelepípedo $ABCDA'B'C'D'$. Esse paralelepípedo é seccionado pelos planos $ADEF$ e $BCEF$, que passam pelos pontos médios $F$ e $E$ das arestas $A'B'$ e $C'D'$, respectivamente. A parte desse paralelepípedo compreendida entre esses planos define o sólido $ABCDEF$, conforme indica a figura a seguir.

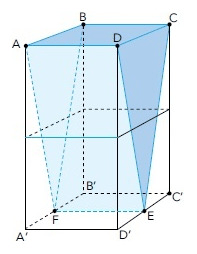
O volume do sólido $ABCDEF$, em $cm^3$, é igual a:

Um anel contém $15$ gramas de ouro $16$ quilates. Isso significa que o anel contém $10\ g$ de ouro puro e $5\ g$ de uma liga metálica. Sabe-se que o ouro é considerado $18$ quilates se há a proporção de $3\ g$ de ouro puro para $1\ g$ de liga metálica.

Para transformar esse anel de ouro $16$ quilates em outro de $18$ quilates, é preciso acrescentar a seguinte quantidade, em gramas, de ouro puro:

Considere a matriz $A_{n\ \times 9}$ de nove colunas com números inteiros consecutivos, escrita a seguir.

$$\boxed{A_{n\ \times 9}=\left[ \begin{array}{ccccccccc} 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 \\ 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 \\ 19 & 20 & 21 & 22 & 23 & 24 & 25 & 26 & 27 \\ 28 & 29 & 30 & 31 & 32 & 33 & 34 & 35 & 36 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array} \right]}$$

Se o número $18.109$ é um elemento da última linha, linha de ordem $n$, o número de linhas dessa matriz é: