MACK 2012 Matemática - Questões

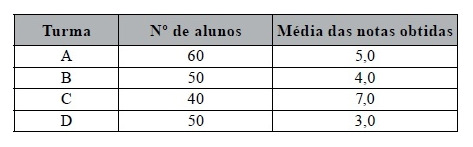
A tabela acima refere-se a uma prova aplicada a $200$ alunos, distribuídos em $4$ turmas $A, B, C\ e\ D$. A média aritmética das notas dessa prova é

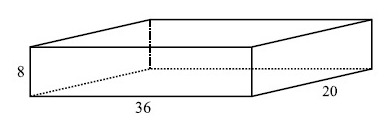
O número mínimo de cubos de mesmo volume e dimensões inteiras, que preenchem completamente o paralelepípedo retângulo da figura, é

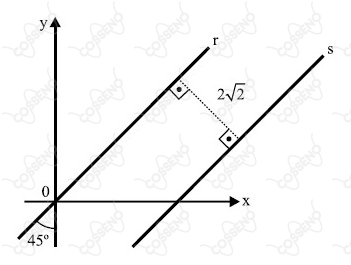
Na figura abaixo, as retas $r$ e $s$ são paralelas. Se $\left(x,\ y\right)$ é um ponto de $s$, então $x-y$ vale

O maior valor que o número real $\dfrac{10}{\left[ 2-\dfrac{\hspace{2pt}\mathrm{sen}\ x}{3} \right] }$ pode assumir é

Na igualdade $y=\sqrt{\log _{\frac{1}{2} } \left(\frac{x}{2} -3\right)}$, supondo $x$ o maior valor inteiro possível, então, nesse caso, $x^{2y}$ vale