ITA 2021 Física - Questões
Abrir Opções Avançadas
O sistema de unidades atômicas de Hartree e bastante útil para a descrição de sistemas quânticos macroscópicos. Nele, faz-se com que a carga fundamental $e$, a massa do elétron $m_0$, a constante eletrostática do vácuo $K_0$ e a constante de Planck reduzida $\hbar$ sejam todas numericamente iguais a unidade. Assinale a alternativa que contém a ordem de grandeza do valor numérico da velocidade da luz no vácuo $c$, nesse sistema de unidades.
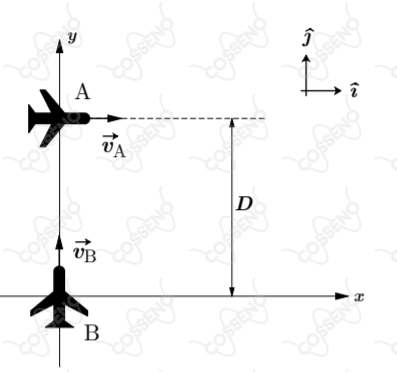
Dois aviões de combate, $A$ e $B$, viajam a uma mesma altitude com velocidades constantes $\vec{v_A} = (100 \ m/s)\hat{i}$ e $\vec{v_B} = (200 m/s)\hat{j}$, respectivamente. A figura ilustra as posições dos aviões no instante $t=0 \ s$, que estão separadas por uma distância $D=100 \ m$. Devido ao funcionamento de sua turbina, o avião $A$ emite um som de frequência característica de $1000 \ Hz$. A velocidade do som na região onde se encontram os aviões é de $300 \ m/s$. Com base nessas informações, calcule:
a) a distância mínima entre os dois aviões ao longo do movimento
b) a frequência percebida no instante $t=0 \ s$, pelo piloto do avião $B$, devido ao som da turbina do avião $A$
Um trem parte do repouso sobre uma linha horizontal e deve alcançar a velocidade de $72 \ km/h$. Até atingir essa velocidade, o movimento do trem tem aceleração constante de $0,50 \ m/s^2$, sendo que resistências passivas absorvem $5,0\%$ da energia fornecida pela locomotiva. O esforço médio, em $N$, fornecido pela locomotiva para transportar uma carga de $1,0 \ ton$ é
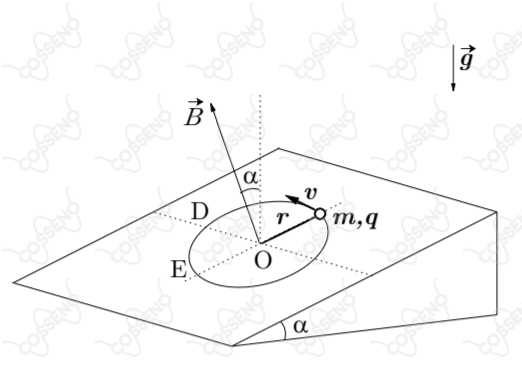
Uma pequena esfera de massa $m$ e carga $+q$ está conectada por um o inextensível preso num ponto $O$ e se move num círculo de raio $r$ sobre um plano liso de inclinação $\alpha$ com a horizontal. Na região existe um campo magnético $\vec{B}$ uniforme e constante, perpendicular ao plano inclinado como ilustra a figura. Se a esfera possui uma velocidade $\vec{v}$ no ponto mais alto da trajetória, determine a tração no fio quando a esfera passa pelas posições $D$ e $E$ indicadas na figura. Considere o sentido de $\vec{v}$ indicado na figura.
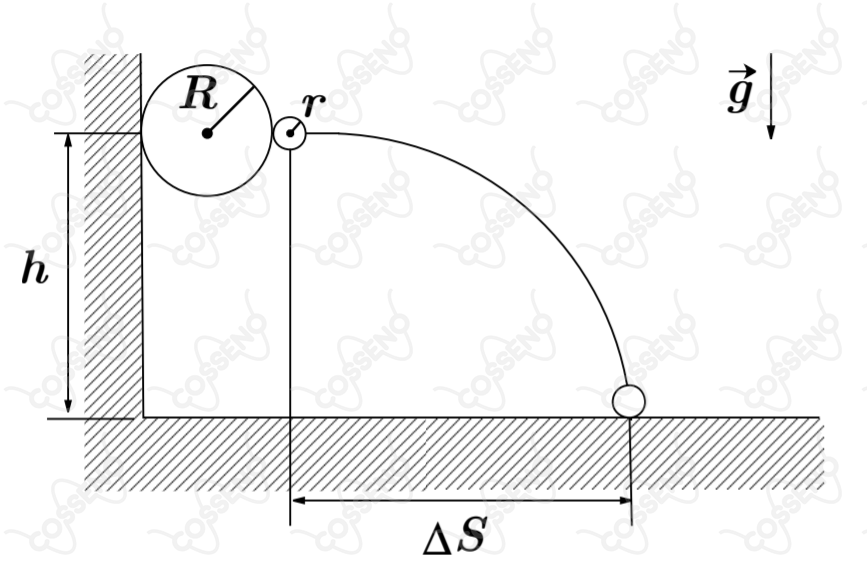
Uma bola de gude de raio $r$ e uma bola de basquete de raio $R$ são lançadas contra uma parede com velocidade horizontal $v$ e com seus centros a uma altura $h$. A bola de gude e a bola de basquete estão na iminência de contato entre si, assim como ambas contra a parede. Desprezando a duração de todas as colisões e quaisquer perdas de energia, calcule o deslocamento horizontal $\Delta S$ da bolinha de gude ao atingir o solo.
Carregando...