ITA 2011 Física - Questões
Abrir Opções Avançadas
Um problema clássico da cinemática considera objetos que, a partir de certo instante, se movem conjuntamente com velocidade de módulo constante a partir dos vértices de um polígono regular, cada qual apontando à posição instantânea do objeto vizinho em movimento. A figura mostra a configuração desse movimento múltiplo no caso de um hexágono regular.
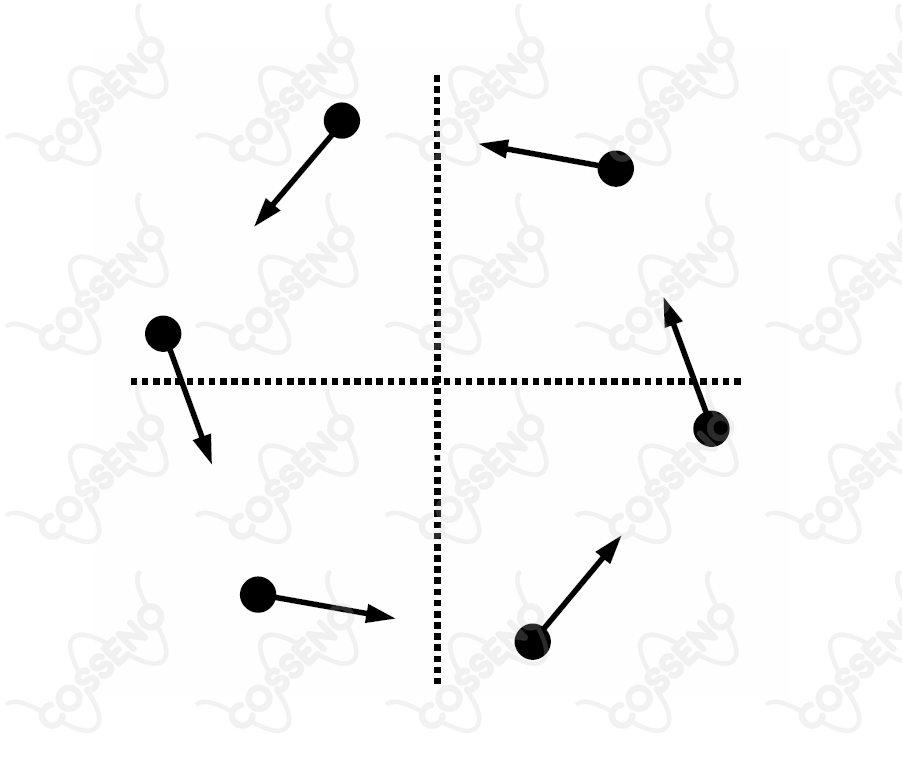
Considere que o hexágono tinha $10{,}0\ m$ de lado no instante inicial e que os objetos se movimentam com velocidade de módulo constante de $2{,}00\ m/s$. Após quanto tempo estes se encontrarão e qual deverá ser a distância percorrida por cada um dos seis objetos?
Um cubo maciço homogêneo com $4{,}0\ cm$ de aresta flutua na água tranquila de uma lagoa, de modo a manter $70\ \%$ da área total da sua superfície em contato com a água, conforme mostra a figura.
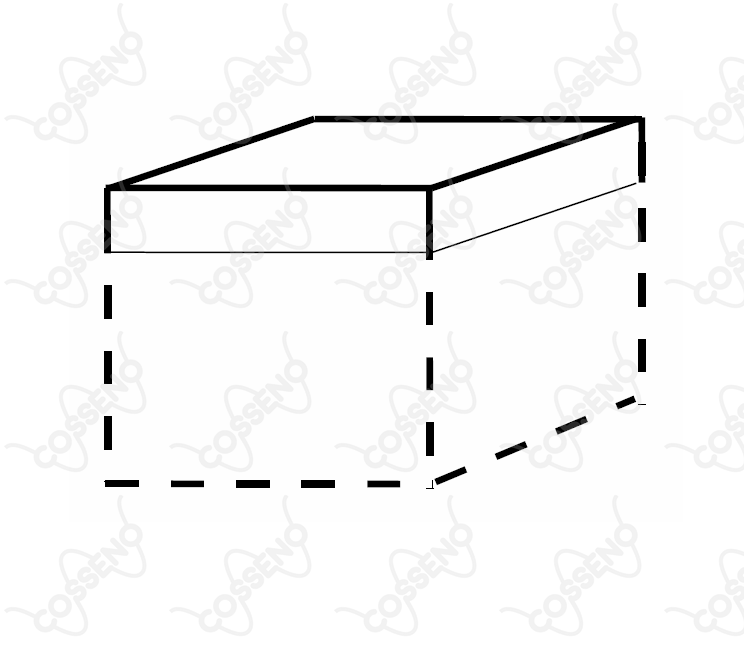
A seguir, uma pequena rã se acomoda no centro da face superior do cubo e este se afunda mais $0{,}50\ cm$ na água. Assinale a opção com os valores aproximados da densidade do cubo e da massa da rã, respectivamente.
Uma pessoa de $80{,}0\ kg$ deixa-se cair verticalmente de uma ponte amarrada a uma corda elástica de "bungee jumping" com $16{,}0\ m$ de comprimento. Considere que a corda se esticará até $20{,}0\ m$ de comprimento sob a ação do peso. Suponha que, em todo o trajeto, a pessoa toque continuamente uma vuvuzela, cuja frequência natural é de $235\ Hz$. Qual(is) é(são) a(s) distância(s) abaixo da ponte em que a pessoa se encontra para que um som de $225\ Hz$ seja percebido por alguém parado sobre a ponte?
Na ficção científica A Estrela, de H.G. Wells, um grande asteróide passa próximo à Terra que, em consequência, fica com sua nova órbita mais próxima do Sol e tem seu ciclo lunar alterado para $80$ dias. Pode-se concluir que, após o fenômeno, o ano terrestre e a distância Terra-Lua vão tornar-se, respectivamente,
Sobre uma mesa sem atrito, uma bola de massa $M$ é presa por duas molas alinhadas, de constante de mola $k$ e comprimento natural $\ell_0$, fixadas nas extremidades da mesa. Então, a bola é deslocada a uma distância $x$ na direção perpendicular à linha inicial das molas, como mostra a figura, sendo solta a seguir.

Obtenha a aceleração da bola, usando a aproximação $(1 + a)^\alpha = 1 + \alpha a$.
Carregando...