ITA 1992 Física - Questões
Abrir Opções Avançadas
Na figura abaixo, a massa esférica $M$ pende de um fio de comprimento $L$, mas está solicitada para a esquerda por uma força $F$ que mantém a massa apoiada contra uma parede vertical $P$, sem atrito. Determine os valores de $F$ e de $R$ (reação da parede), respectivamente.
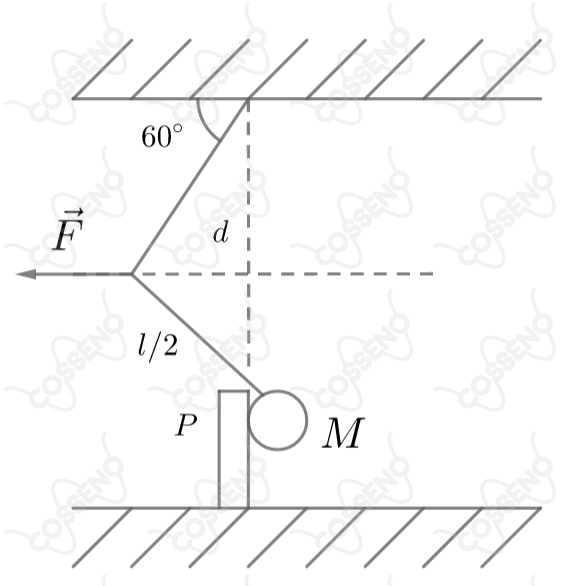
Na Questão 01:
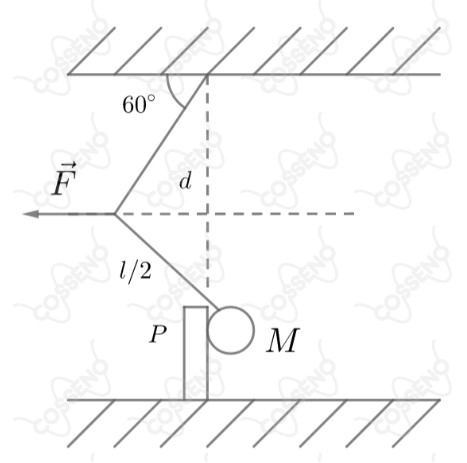
A) Calcule o trabalho $W$ realizado pela força $F$ para fazer subir lentamente ($V=0$) a massa $M$ em termos da variação da energia potencial de $M$, desde a posição em que o fio está na vertical até a situação indicada no desenho.
B) Verifique se é possível calcular esse trabalho como o produto de $F$, já calculada, pelo deslocamento $d$.
Responda A e B, respectivamente.
Dois automóveis que correm em estradas retas e paralelas têm posições a partir de uma origem comum, dadas por: $$X_1 = (30t)\ m$$$$X_2 = (1,0 . 10^{3}+ 0,2t^{2})\ m$$Calcule o(s) instante(s) $t$ e ($t’$), respectivamente, em que os dois automóveis devem estar lado a lado.
Um bloco de massa igual a $5,0\ kg$ é puxado para cima por uma força $F = 50\ N$ sobre o plano inclinado da figura, partindo do repouso.
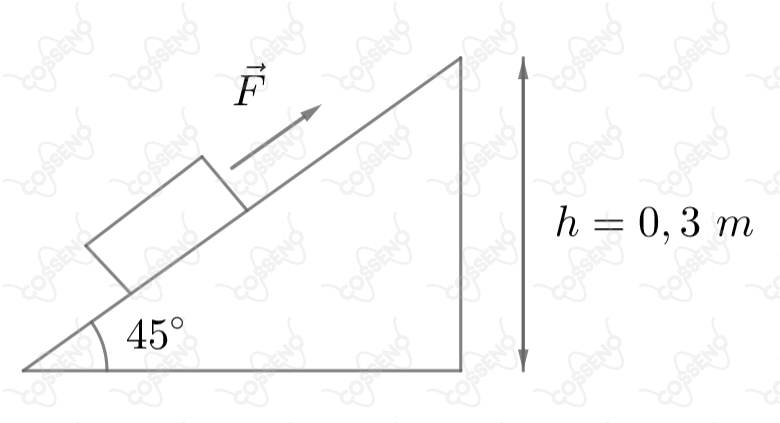
a) Calcule a energia cinética com que o bloco chega ao topo do plano. ($E_c\ [J]$)
b) Calcule a aceleração do bloco. ($a\ [m/s^2]$)
c) Escreva a velocidade do bloco em função do tempo. ($v\ [m/s]$)
O coeficiente de atrito cinético plano- bloco é $\mu = 0,25$.
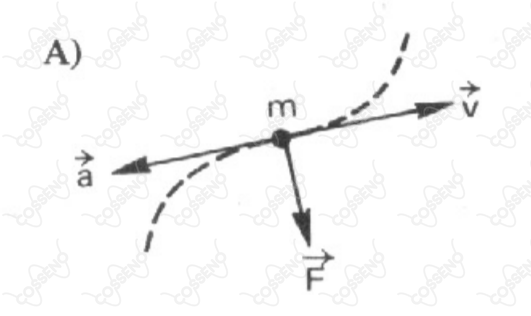
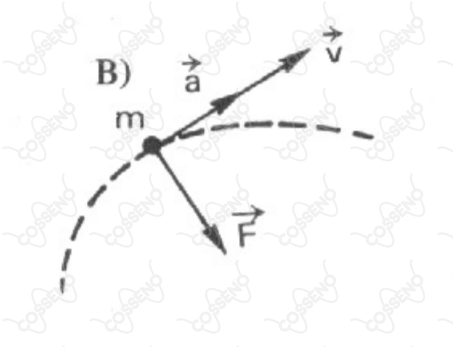
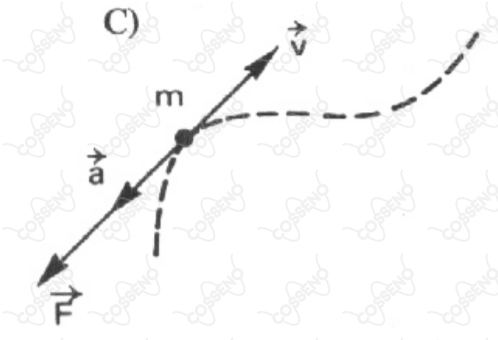
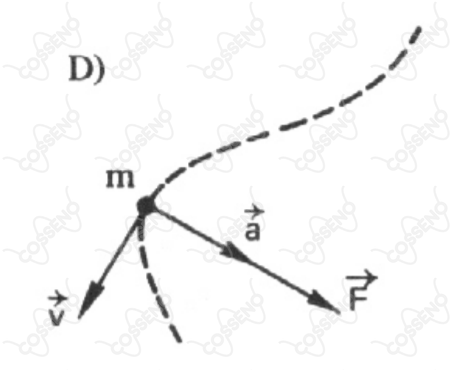
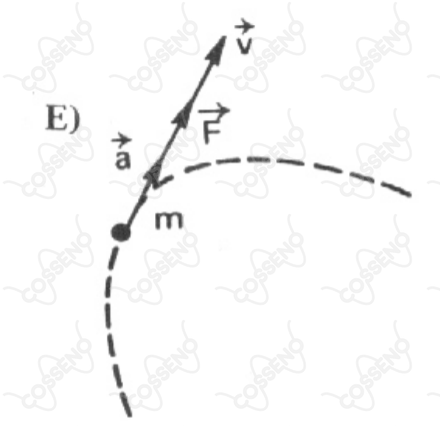
Seja $\vec{F}$ a resultante das forças aplicadas a uma partícula de massa m, velocidade $\vec{V}$ e aceleração $\vec{a}$ . Se a partícula descrever uma trajetória plana, indicada pela curva tracejada em cada um dos esquemas a seguir, seguese que aquele que relaciona corretamente os vetores coplanares, e é:
Carregando...