IME 2011 Matemática - Questões
Abrir Opções Avançadas
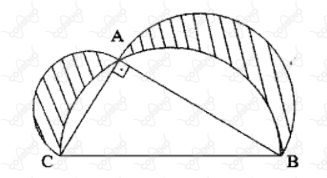
Seja o triângulo retângulo $ABC$ com os catetos medindo $3\ cm$ e $4\ cm$. Os diâmetros dos três semicírculos, traçados na figura abaixo, coincidem com os lados do triângulo $ABC$. A soma das áreas hachuradas, em $cm^2$, é:
A base de um prisma reto $ABCA_1B_1C_1$ é um triângulo com o lado $AB$ igual ao lado $AC$. O valor do segmento $CD$ vale $x$, onde $D$ é o ponto médio da aresta lateral $AA_1$. Sabendo que $\alpha$ é o ângulo $ACB$ e $\beta$ é o ângulo $DCA$, determine a área lateral do prisma em função de $x$, $\alpha$ e $\beta$.
O valor de $x$ que satisfaz a equação $\sin (\arctan (1 + x)) = \cos(\arctan(x))$:
Determine o valor da excentricidade da cônica dada pela equação $x^2 - 10\sqrt3 xy + 11y^2 + 16 = 0$.
A base de uma pirâmide é um retângulo de área $S$. Sabe-se que duas de suas faces laterais são perpendiculares ao plano da base. As outras duas faces formam ângulos de $30^\circ$ e $60^\circ$ com a base. O volume da pirâmide é;
Carregando...