IME 2008 Matemática - Questões
Abrir Opções Avançadas
De quantas maneiras $n$ bolas idênticas podem ser distribuídas em três cestos de cores verde, amarelo e azul?
Determine o conjunto-solução da equação $$sin^{3}{x} + \cos^{3}{x} = 1 - \sin^{2}{x} \cdot \cos^{2}{x}$$
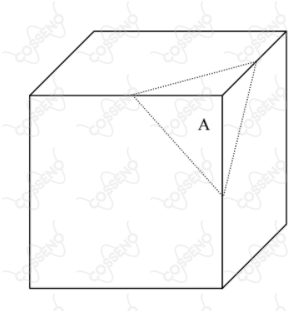
Um plano corta um cubo com aresta de comprimento $1$ passando pelo ponto médio de três arestas concorrentes no vértice A e formando uma pirâmide, conforme a figura a seguir. Este processo é repetido para todos os vértices. As pirâmides obtidas são agrupadas formando um octaedro cuja área da superfície externa é igual a:
Encontre o polinômio $P(x)$ tal que $Q(x) + 1 = (x - 1)^3 \cdot P(x)$ e $Q(x) + 2$ é divisível por, onde $Q(x)$ é um polinômio do $6^{\circ}$ grau.
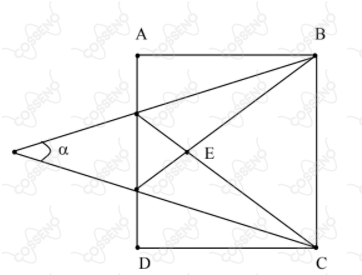
Na figura seguinte $ABCD$ é um quadrado de lado $1$ e $BCE$ é um triângulo equilátero. O valor de $\tan\left(\frac{\alpha}{2}\right)$ é igual a:
Carregando...