IME 2005 Física - Questões
Abrir Opções Avançadas
Um canhão de massa $M = 200\ kg$ em repouso sobre um plano horizontal sem atrito é carregado com um projétil de massa $m = 1\ kg$, permanecendo ambos neste estado até o projétil ser disparado na direção horizontal. Sabe-se que este canhão pode ser considerado uma máquina térmica com $20\%$ de rendimento, porcentagem essa utilizada no movimento do projétil, e que o calor fornecido a esta máquina térmica é igual a $100.000\ J$. Suponha que a velocidade do projétil após o disparo é constante no interior do canhão e que o atrito e a resistência do ar podem ser desprezados. Determine a velocidade de recuo do canhão após o disparo.
Considere um elétron de massa $m$ e carga $-e$, que se move com velocidade $v$ conforme indicado na figura abaixo. No instante $t = 0$ é ligado um campo magnético $B$ uniforme em todo o espaço. Desprezando a ação da gravidade, determine:
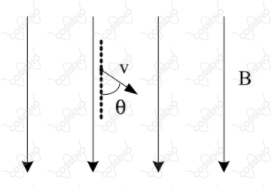
a) o trabalho realizado pela força magnética após um intervalo de tempo $\Delta t$ .
b) o período do movimento no plano perpendicular a $B$.
c) a trajetória seguida pelo elétron, graficamente.
Um fio condutor rígido $PQR$, dobrado em ângulo reto, está ortogonalmente inserido em um campo magnético uniforme de intensidade $B=0{,}40\ T$. O fio está conectado a dois circuitos, um resistivo e o outro capacitivo. Sabendo que o capacitor $C_1$ está carregado com $40\ \mu C$, determine a intensidade da força de origem magnética que atuará sobre o fio $PQR$ no instante em que a chave $K$ for fechada.
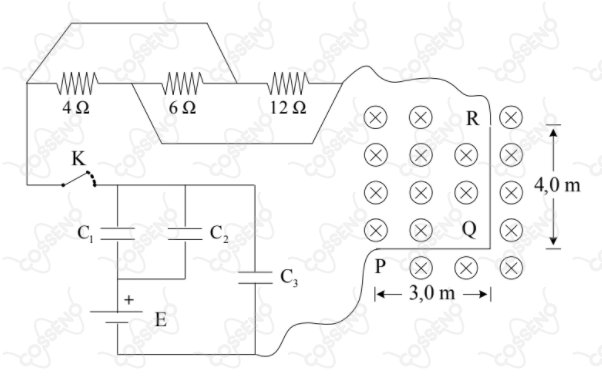
$C_2 = 2\ \mu F$ e
$C_3 = 6\ \mu F$
Uma corda é fixada a um suporte e tensionada por uma esfera totalmente imersa em um recipiente com água, como mostra a figura. Desprezando o volume e a massa da corda em comparação com o volume e a massa da esfera, determine a velocidade com que se propaga uma onda na corda.

densidade linear da corda $(\mu)= 1{,}6\ g /m$
massa da esfera $(m) = 500\ g$
volume da esfera $(V) = 0{,}1\ dm$
massa específica da água $(d)$ $=1.000\ kg / m$.
Um corpo de massa $m$ e volume $v= 1\ m^3$, imerso em um líquido de massa específica $\rho_0$, é solto, inicia o movimento vertical, atinge o anteparo $A$ e provoca uma deformação máxima $x$ na mola de constante elástica $k$. Em seguida, o procedimento é repetido, porém com líquidos de massa específica $\rho_1$ diferente de $\rho_0$. O gráfico abaixo mostra a relação entre a variação da massa específica do líquido $\Delta \rho$ e a variação da deformação máxima da mola $\Delta x$.


a) Construa o gráfico da deformação máxima da mola $x$ em função da diferença entre as massas específicas do corpo e do líquido $\Delta \rho_{CL}$.
b) Determine o valor de $x$ para $\Delta \rho_{CL} = 1.000\ kg/m^3$.
Carregando...