IME 1995 - Questões
Abrir Opções Avançadas
Dado $Z = \frac{1}{\sqrt{7 + 24i}}$, calcule as partes real e imaginária de $Z$.
Resolva a equação trigonométrica: $$\sin{x} + \cos{x} + 2 \sqrt{2} \sin{x} \cos{x} = 0$$
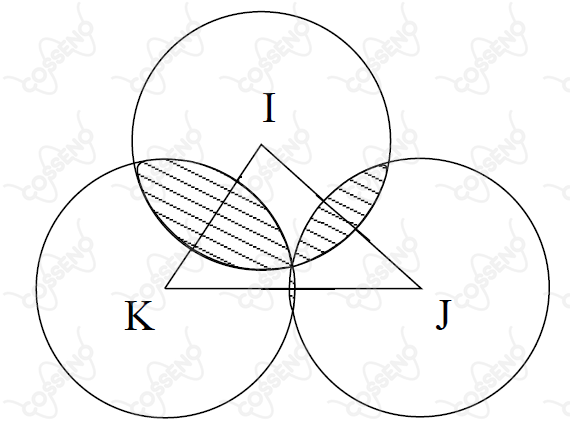
Três círculos de raio $R$ se interceptam dois a dois, como é mostrado na figura abaixo, constituindo três áreas comuns que formam um trevo. Determine o perímetro do trevo e sua área em função de $R$ e da área $S$ do triângulo $IJK$.
Seja $ABC$ um triângulo qualquer no qual os vértices $B$ e $C$ são fixos. Determine o lugar geométrico descrito pelo ponto $A$, variável, sabendo que os ângulos $B$ e $C$ satisfazem a relação $\tan{B} \tan{C} = k$, $k$ constante real. Discuta a solução para os diversos valores de $k$.
Seis esferas idênticas de raio $R$ encontram-se posicionadas no espaço de tal forma que cada uma delas seja tangente a quatro esferas. Dessa forma, determine a aresta do cubo que tangencie todas as esferas.
Carregando...