IME 1992 Matemática - Questões

Prove que $\overline{Z_1 + Z_2} = \overline{Z_1} +\overline{ Z_2}$, onde $Z_1$ e $Z_2 \in \mathbb{C}$.

Encontre todas as soluções de:$$ \sec x - 2 \cos x = 1 \ \  \text{ em $[0, 2\pi]$}$$

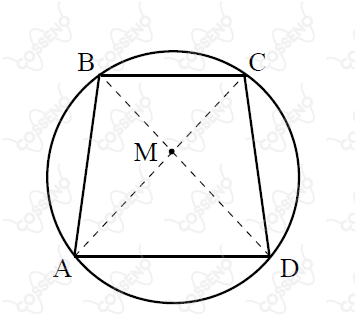
Dado o quadrilátero $ABCD$, inscrito num círculo de raio $r$, conforme a figura abaixo, prove que:$$\frac{AC}{BD} = \frac{AB\cdot AD + BC\cdot CD} {AB\cdot BC + CD\cdot AD}$$

Calcule quantos números naturais de $3$ algarismos distintos existem no sistema de base $7$.

Determine a equação da reta que passa por um dos vértices da curva definida por $4y^2 + 8y – x^2 = 4$, formando um ângulo de $45^\circ$ com o eixo horizontal.