ESPCEX 2012 Matemática - Questões
Abrir Opções Avançadas
Considere a circunferência $(\lambda) x^{2} + y^{2} - 4x = 0$ e o ponto $P(1, \sqrt{3})$. Se a reta $t$ é tangente a $\lambda$ no ponto $P$, então a abscissa do ponto de intersecção de $t$ com o eixo horizontal do sistema de coordenadas cartesianas é
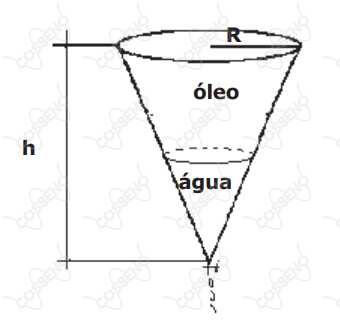
Um recipiente em forma de cone circular reto, com raio da base $R$ e altura $h$, está completamente cheio com água e óleo. Sabe-se que a superfície de contato entre os líquidos está inicialmente na metade da altura do cone. O recipiente dispõe de uma torneira que permite escoar os líquidos de seu interior, conforme indicado na figura. Se essa torneira for aberta, exatamente até o instante em que toda água e nenhum óleo escoar, a altura do nível do óleo, medida a partir do vértice será
A probabilidade de se obter um número divisível por $2$ na escolha ao acaso de uma das permutações dos algarismos $1$, $2$, $3$, $4$, $5$ é
A figura geométrica formada pelos afixos das raízes complexas da equação $x^{3} - 8 = 0$ tem área igual a
Se $\frac{6 - log_{a} m}{1 + log_{a^{2}} m} = 2$, com $a > 0$, $a \neq 1$ e $m > 0$, então o valor de $\frac{\sqrt{m}}{a + \sqrt{m}}$ é
Carregando...