ESPCEX 2005 Física - Questões
Abrir Opções Avançadas
A figura abaixo mostra a trajetória de um feixe de luz monocromático que vem de um meio I, atravessa os meios II e III, é totalmente refletido na interface dos meios III e IV. Os ângulos $\alpha$, $\beta$ e $\gamma$ são os ângulos formados entres as normais às superfícies de separação dos meios e o feixe de luz monocromático, sendo $\alpha > \gamma > \beta $. Os meios são homogêneos, transparentes, estão em equilíbrio estático e as interfaces são planas e paralelas.
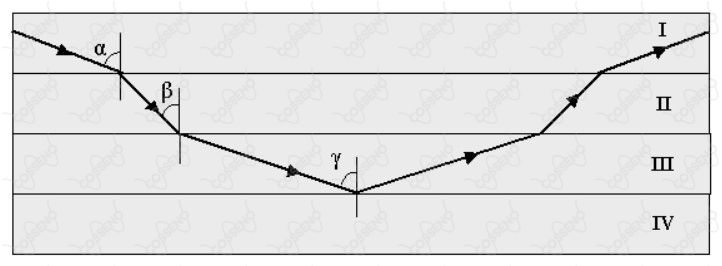
Sabe-se que o índice de refração absoluto do vidro é maior que o da água e que o índice de refração absoluto da água é maior que o do ar. Baseado nestas informações é correto afirmar que os meios I, II, III e IV podem ser, respectivamente:
Um cozinheiro necessita preparar $\pu{1,5 litros}$ de café com leite a uma temperatura de $\pu{42ºC}$. Ele dispõe de $\pu{700 mililitros}$ de café a $\pu{82ºC}$. Considerando que somente haja troca de calor entre o café e o leite e que ambos tenham o mesmo calor específico e a mesma densidade, para conseguir o seu intento, a temperatura inicial do leite que será misturado ao café deve ser de:
Um bloco parte da posição $1$ e desloca-se em movimento retilíneo uniformemente variado sobre uma superfície horizontal com atrito até parar na posição $3$, conforme a figura abaixo.

Desprezando a resistência do ar, o diagrama que melhor representa todas as forças que atuam sobre o bloco, quando ele está passando pelo ponto $2$, é:
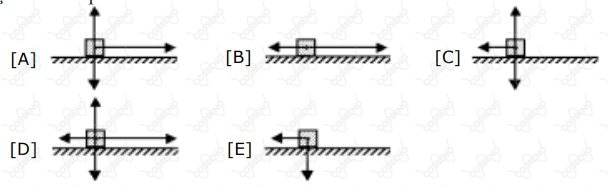
Obs.: Todas as forças estão representadas no centro de massa do bloco.
Em um sistema massa-mola ideal, sem forças dissipativas, a freqüência de oscilação $f$ de uma massa $m$ é dada por $f = \frac{1}{2\pi}\sqrt{\frac{k}{m}}$ , onde $k$ representa a constante elástica da mola. Nos sistemas A e B representados abaixo, as forças dissipativas são nulas, as molas são ideais, $X_1$ e $X_2$ representam a posição de elongação máxima das molas e as massas $m_1$ e $m_2$ são iguais. Para que a situação indicada na figura se repita a cada 3 oscilações do sistema A e 2 oscilações do sistema B, a razão entre $k_1$ e $k_2$ é igual a:

Uma mola ideal de constante elástica $k = \pu{256 N/m}$ está presa a um anteparo fixo e é comprimida de $\pu{0,5 m}$ contra ele por um bloco A de massa $\pu{2 kg}$. O bloco A não está preso à mola e se apoia sobre uma superfície horizontal e sem atrito. Soltando-se a mola, esta empurra o bloco ao longo da superfície até perderem o contato entre si. O bloco prossegue deslizando até realizar um choque perfeitamente inelástico com um bloco B de massa $\pu{2 kg}$, inicialmente em repouso, conforme a figura abaixo.

Desprezando todas as forças dissipativas, pode-se afirmar que a velocidade final dos dois blocos será de:
Carregando...