ESPCEX 1996 - Questões

Sabendo que $\log M + \log N = 0$, pode-se afirmar que:

A soma e o produto das raízes da equação $(2^{x + 6})^{ x^{2} - 6x + 5 } = 1$ são, respectivamente:

Numa pesquisa feita junto a $200$ universitários sobre o hábito de leitura de dois jornais ($A$ e $B$), chegou-se às seguintes conclusões:

(1) $80$ universitários lêem apenas um jornal;

(2) o número dos que não lêem nenhum dos jornais é o dobro do número dos que lêem ambos os jornais.

(3) o número dos que lêem o jornal $A$ é o mesmo dos que lêem apenas o jornal $B$.

Com base nesses dados, podemos afirmar que o número de universitários que lêem o jornal $B$ é:

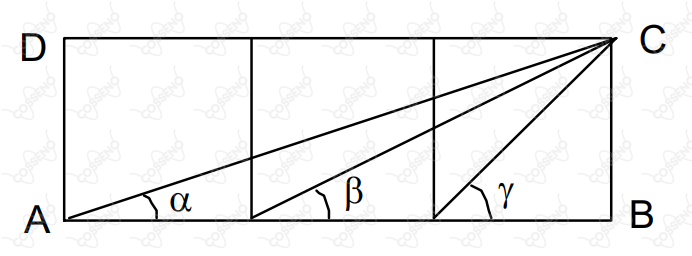
O retângulo $ABCD$ está dividido em três quadrados, como mostra a figura abaixo. Nestas condições, pode-se concluir que $\alpha + \beta$ vale:

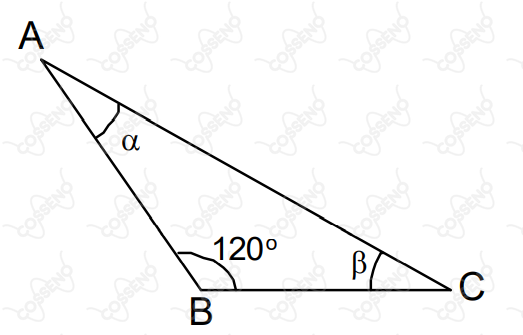
Da figura abaixo, sabe-se que $\cos{\beta} = \frac{\sqrt{2}}{2}$. Então, o $\cos{\alpha}$ vale: